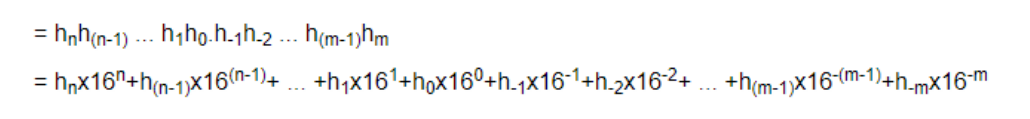In this class, we will write programs.

But first, what is a program?

A program is a sequence of instructions that specifies how to perform a computation.

Every program you've ever used, no matter how complicated, is made up of small instructions that look much like the following:

• input: get data from the keyboard, a file, a sensor, or some other device


• output: display data on the screen, or send data to a file or other device.


• math: perform basic mathematical operations like addition and division.


• decisions: check for certain conditions and execute the appropriate code


• repetition: perform some action repeatedly, usually with some variation.

We can think of programming as the process of: breaking down a large, complex task into smaller and smaller subtasks.

The process continues until the subtasks are simple enough to be performed with the basic instructions provided by the computer.

One of the most interesting aspects of writing programs is deciding how to solve a particular problem, especially when there are multiple solutions.

In order to determine which way is best for a given situation, we need techniques for describing and analyzing solutions formally.

Computer science is the science of algorithms, including their discovery and analysis.

An algorithm is a sequence of steps that specifies how to solve a problem.

• Some algorithms are faster than others, and some use less space in computer memory.

Designing algorithms and writing code is difficult and error-prone.

For historical reasons, programming errors are called bugs, and the process of tracking them down and correcting them is called debugging.

The programming language you will learn in this class is Java, which is a high-level language.

A high-level language is any programming language that enables development of a program in a much more user-friendly programming context and is generally independent of the computer's hardware architecture.

Other high-level languages you may have heard of include:

• Python
• C and C++
• Ruby
• JavaScript

High-level languages have two advantages:

1. It is much easier to program in a high-level language.
• Programs take less time to write, they are shorter and easier to read, and they are more likely to be correct.


2. High-level languages are portable, meaning they can run on different kinds of computers with few or no modifications.
• Low-level programs can only run on one kind of computer, and have to be rewritten to run on another.

• An interpreter reads a high-level program and executes it, meaning that it does what the program says. It processes the program a little at a time, alternately reading lines and performing computations


• A compiler reads the entire program and translates it completely before the program starts running. In this context, the high-level program is called the source code, and the translated program is called the object code or the executable. Once a program is compiled, you can execute it repeatedly without further translation. As a result, compiled programs often run faster than interpreted programs.

As aforementioned, Java is a high-level, class-based, object-oriented programming language and software platform that runs on billions of devices, including notebook computers, mobile devices, gaming consoles, medical devices and many others. The rules and syntax of Java are based on the C and C++ languages.

Here are some specific examples of real world applications that use Java:

• LinkedIn
• Minecraft
• Amazon Web Services (AWS)

To create an application using Java, you will need:

• to download and install the Java Development Kit (JDK), which is available for Windows, macOS, and Linux.


• A command-line interface (CLI) on your computer that allows you to create and delete files, run programs, and navigate through folders and files (On a Mac, it's called Terminal, and on Windows, it's Command Prompt) OR an integrated development environment (IDE) - a software application that helps programmers develop software code efficiently by combining capabilities such as software editing, building, testing, and packaging in an easy-to-use application, such as Eclipse, NetBeans, IntelliJ, DrJava, etc.

You write the program in the Java programming language, then a compiler turns the program into Java bytecode—the instruction set for the Java Virtual Machine (JVM) that is a part of the Java runtime environment (JRE). Java bytecode runs without modification on any system that supports JVMs, allowing your Java code to be run anywhere. The Java software platform consists of the JVM, the Java API, and a complete development environment. The JVM parses and runs (interprets) the Java bytecode.



The Java API consists of an extensive set of libraries including basic objects, networking and security functions; Extensible Markup Language (XML) generation; and web services. Taken together, the Java language and the Java software platform create a powerful, proven technology for enterprise software development.

To start programming in Java, we can write a simple program that outputs "Hello, World!" on the screen. Since it's a very simple program, it's often used to introduce a new programming language to a newbie! 😃

Let's explore how Java "Hello, World!" program works:

// Our First Program
public class HelloWorld {
    public static void main(String [] args) {
        System.out.println("Hello, World!");
    }
}

How does the "Hello, World!" program work?

1. In Java, any line starting with // is a single-line comment (We will learn more about multi-line comments in a bit). Comments are intended for users reading the code to understand the intent and functionality of the program. It is completely ignored by the Java compiler (an application that translates Java program to Java bytecode that computer can execute).


2. Every application begins with a class definition. In this particular program, HelloWorld is the name of the class and the name of the class should match the filename in Java.


3. Next is the main method. Every application in Java must contain the main method. The Java compiler starts executing the code from the main method, and it's mandatory in each of our executable Java programs. The signature of the main method in Java is:
   
   public static void main(String [] args) { ... }


4. Lastly, we have a print statement. It prints the text Hello, World! to standard output (your screen). The text inside the quotation marks is called a String literal in Java. Notice the print statement is inside the main function, which is inside the class definition.

Comments have no effect on the execution of the program, but they make it easier for other programmers (and yourself!) to understand what you meant to do and how the program works.

There are three types of comments:

• // single line comments


• /*
  multiline comments
  */


• /**
  multiline Documentation Comments to create formal documentation using Javadoc
  */

First we identify the necessary keyword for the variable datatype. For example, a whole number should be declared as an integer type known as int while a decimal number should be declared as a float or double.

int score = 42; 

In the previous example, we have assigned value to the variable during declaration -- this is known as initialization, because we assign an initial value to a variable.

However, we can also declare variables and assign variables separately.

For example:

int score;
score = 42;

When you declare a variable, you create a named storage location.

When you make an assignment to a variable, you update its value.

The value of a variable can be modified throughout the program (that's what makes it a variable, opposed to a literal)

For example:

int score = 0;
//more code to be added here
score = 42;

Here, initially, we set the score to 0.

Later (after some more code -- not yet specified) we changed it to 42.

It is important to remember, however, that we CANNOT change the data type of a variable in Java within the same scope (we'll discuss scope a bit more later, for now just think of our scope limited to the main method)

We can display the value of a variable using print or println.

int score = 42;
//What should be printed below?
System.out.println(score);

The scope of a variable is the part of the program where the variable is accessible.

In general, a set of curly brackets { } defines a scope.

A variable declared inside pair of brackets “{” and “}” in a method is only accessible within the scope of the brackets only. (This will make more sense when we explore conditional statements, loops, methods, etc.)

We can also declare variables directly inside the class (outside any specific method -- we will revisit this once we begin writing more methods).

These variables can be directly accessed anywhere in class.

Operators are symbols that perform operations on variables and values. For example, we know that + is an operator used for addition, while * is an operator used for multiplication.

Operators in Java can be classified into the following types:

1. Arithmetic Operators
• Arithmetic operators are used to perform arithmetic operations on variables and data.
• The various arithmetic operators we use include:
• + (Addition, e.g. a + b)
• - (Subtraction, e.g. a - b)
• * (Multiplication, e.g. a * b)
• / (Division, e.g. a / b)
• % (Modulus -Remainder after division, e.g. a % b)
• ++ (Increment, e.g. a++ or ++a)
• -- (Decrement, e.g. a-- or --a)


2. Assignment Operators
• Assignment operators are used in Java to assign values to variables.
• A few assignment operators available in Java include:
• = (Assignment, e.g. a = b)
• += (Additional assignment, e.g. a += b is equivalent to a = a + b)
• we can also write assignment operators for other arithmetic operations such as subtraction, multiplication, division, modulus, etc.


3. Relational (or Comparison) operators
• Relational/Comparison operators are used to compare two values (or variables). The values returned from comparison are known as boolean values and will either be true or false.
• A few relational/comparison operators available in Java include:
• == (Equal to, e.g. a == b)
• != (Not equal to, e.g. a != b)
• > (Greater than, e.g. a > b)
• < (Less than, e.g. a < b)
• >= (Greater than or equal to, e.g. a >= b)
• <= (Less than or equal to, e.g. a <=b)


4. Logical Operators
• Logical operators are used to determine the logic (whether a statement is true or false) between variables or values.
• A few logical operators available in Java include:
• && (Logical and - returns true if both statements are true, e.g. a < 5 && b < 5)
• || (Logical or - returns true if one of the statements is true, e.g. a < 5 || b < 5)
• ! (Logical not - reverses the result, returns false if the result is true, e.g. !(a < 5 && b < 5)))


5. Unary Operators
• Unary operators are operators that need only one operand to perform any operation, such as: increment, decrement, negation, etc. It consists of various arithmetic, logical and other operators that operate on a single operand.
• A few unary operators available in Java include:
• + (Unary Plus - represents a positive value, e.g. +a)
• - (Unary Minus - represents a negative value, e.g. -a)
• ! (Greater than or equal to, e.g. a >= b)
• ++ (Increment Operator - increments the value of a variable by 1, e.g. ++a OR a++)
• -- (Decrement Operator - decrements the value of a variable by 1, e.g. --a OR a--)
• The last previous two operators (increment and decrement) are especially important because not only are they incredibly useful in multiple cases but they also have two variants of these operators:
1. Pre-increment/decrement (also known as prefix)
• Here our code increments/decrements the value first, and then performs the specified operation.

// Prefix increment example
public class PrefixExample {
    public static void main(String [] args) {
        int a = 5;
        System.out.println(++a);//this immediately increments to 5+1 and prints 6
        System.out.println(a);//this reflects the modifcation in the previous line AND also prints 6
    }
}

2. Post-increment/decrement (also known as postfix)
• Here our code performs the specified operation first, and then increments/decrements the value.

// Postfix increment example
public class PostfixExample {
    public static void main(String [] args) {
        int a = 5;
        System.out.println(a++);//prints the current value of a (5) BEFORE incrementing
        System.out.println(a);//value has been printed out, incremented, now prints 6
    }
}



6. Bitwise Operators

TO REMEMBER:

Floating-point numbers in Java are used to represent fractional values or numbers with a large range of possible values. They are primarily used when precise decimal calculations are not required.

Java uses two primitive data types to represent floating-point numbers: float and double.

• The float data type is a 32-bit single-precision floating-point number
• The double data type (which we will use in this class rather than float) is a 64-bit double-precision floating-point number. This makes the double data type more accurate than the float data type.

We can create double variables and assign values to them using the same syntax we used for the other types:

double payRate = 42.5;

The simplest way to convert a floating-point value to an integer is to use a type cast, so called because it molds or “casts” a value from one type to another.

The syntax for type casting is to put the name of the type in parentheses and use it as an operator.

double payRate = 42.5;
int pay = (int) payRate;

What is the value of the variable pay?

In math, division often allows for remainders. It is why whenever a number is NOT evenly divisible by another number it can result in a decimal number opposed to a whole number e.g. 5/2 is equal to 2.5

However, integer division and division as we know from math class (also known as floating-point division) are two different ways of performing division operations.

Integer division is the division operation performed on two integers, resulting in an integer quotient. The result is obtained by discarding the fractional part of the division, if any. In other words, it performs a "round towards zero" operation.

• For example, if you perform an integer division of 10 divided by 3, the result is 3 because it discards the fractional part.
• Similarly, if you divide -10 by 3 using integer division, the result is -3, as it still rounds towards zero.

In Java, when dividing two integers using the '/' operator, integer division is performed if both operands are integers.

To perform floating-point division, at least one of the operands should be a floating-point number.

For example:

int result = 10 / 3;//Integer division, result is 3
double result = 10.0 / 3;//Regular division, result is approximately 3.3333

It is important to be aware of the distinction between integer division and floating-point division, especially when working with different data types and when precision is required in calculations.

Java has a lot of built-in Math methods that allow us to perform more complex mathematical computations. The Math class is found in the java.lang package, so you don't have to import it.

For example, if you need to get the square root of a number, we use the Math.sqrt() method.

Some frequently used Math class methods include:

• Math.abs(n) - for computing the absolute value of a particular number
• Math.sqrt(n) - for computing the square root of a particular number
• Math.pow(base, exp) - for computing the result of a particular base raised to the power of a particular exponent

Although not a method, Math.PI - is a static final double constant in Java, equivalent to in π Mathematics

You can learn more about the Java Math class methods from the Java API here

Most computer programs do the same thing every time they run, meaning they are deterministic. Usually we want our programs to be deterministic since we expect the same calculation to yield the same result. But for certain applications (e.g. games) we want to write programs that are nondeterministic.

It is hard for a computer to generate truly random numbers. But there are algorithms that generate unpredictable sequences called pseudorandom numbers. For most applications, they are as good as random.

The Math.random() method returns a pseudorandom double type number between 0.0 and 1.0, where 0.0 is inclusive and 1.0 is exclusive.

When this method is first called, it creates a single new pseudorandom-number generator

public class RandomExample {
    public static void main(String [] args) {
        double rand = Math.random();//Generate random number
        System.out.println("Random Number:" + rand);//different each run
    }
}

to generate a random number in range:

There are three types of errors can occur in a program:

1. Compiler errors
2. Run-time errors
3. Logic errors

Compiler errors occur when you violate the syntax rules of the Java language. For example, forgetting a semicolon at the end of a statement or that parentheses and braces have to come in matching pairs. So (1 + 2) is legal, but 8) is not. In the latter case, the program cannot be compiled, and the compiler displays an error.

• Error messages from the compiler usually indicate where in the program the error occurred, and sometimes they can tell you exactly what the error is.

Run-time errors occur while the interpreter is executing byte code and something goes wrong. These errors are also called “exceptions” because they usually indicate that something exceptional (and bad) has happened. (Example: attempting divide by zero)

• When a run-time error occurs, the interpreter displays an error message that explains what happened and where.

The third type of error is the logic error. If your program has a logic error, it will compile and run without generating error messages, but it will not do the right thing. Instead, it will do exactly what you told it to do (even if it isn't the right solution).

• Usually the compiler and the interpreter CANNOT help you, since they don't know what the right thing is.

So far we have used System.out.println() to display text to the screen. But what does it actually mean?

System is a class (that belongs to the java.lang package, which is imported automatically) that provides methods related to the “system” or environment where programs run.

System.out represents the Standard Output Stream. That means that if we want to print any statement on the console, we should use the following statement:

System.out.print();

There are three methods we use to print statements:

1. print(String s)
• Used to print on the console.
• Accepts a String as a parameter (we can concatenate parts to the String if necessary, i.e. “Hello” + “ World”, etc. however, it is typical convention to include all string literals in the same pair of quotations if they are consecutive)
• After printing the statement, the cursor remains on the same line.


2. println(String s)
• An upgraded version of the print() method, also used to display text on the console.
• After printing the statement, it throws the cursor at the start of the next line.


3. printf(String format, datatype args)
• Accepts two parameters:
• format: It is a formatted String, uses placeholders with specific conversion characters to refer to the arguments that will be replaced when printing
• args: It is an argument referenced by the format specifiers. If the number of arguments is more than the format specifiers, the other arguments are ignored. The number of arguments may be zero.

A formatted placeholder is declared as follows:

%[flags][width][.precision]conversion-character

With any flags, width, and precision as optional modifiers

Feel free to consult the following:



printf() throws:

• a NullPointerException if the format is null
• an IllegalFormatException if a format string contains illegal syntax
• an IllegalFormatConversionException if the placeholder and corresponding argument are not of the same type

The \n is an escape sequence, which is a sequence of characters that represents a special character. The backslash allows you to “escape” the string's literal interpretation.

As we previously discussed, a variable in Java must be declared as a specific data type. These data types are divided into two groups:

• Primitive Data Types, which specify the size and type of variable values and has no additional methods

AND

• Non-primitive data types, also called reference types because they refer to objects

Primitive Data Types

The main difference between primitive and non-primitive data types are:

• Primitive types are predefined (already defined) in Java. Non-primitive types are created by the programmer and is not defined by Java (except for String)


• Non-primitive types can be used to call methods to perform certain operations, while primitive types cannot.


• A primitive type has always a value, while non-primitive types can be null.


• A primitive type starts with a lowercase letter, while non-primitive types starts with an uppercase letter. (e.g. Strings, etc.)

We will revisit the concept of Strings in depth a bit later but for now just know that Strings contain a sequence of "characters" strung together.

Characters can be letters, numbers, punctuation marks, symbols, spaces, tabs, etc.

We can initialize a String simply by stating:

String s = "Hello";

In most cases, we can use a String as a variable data type just like we have for int, double, etc. (Although all Strings we create are technically objects and have more behaviors than the primitive data types -- but we'll talk more about that later)

In general, you cannot perform mathematical operations on strings, even if the strings look like numbers. The following expressions are illegal:

• "Hello" - 1
• "World" / 123
• "Hello" * "World"

However, the + operator DOES work with strings.

For strings, the + operator performs concatenation, which means joining end-to-end.

So "Hello, " + "World!" yields the string "Hello, World!".

Or if you have a variable called name that has type String, the expression "Hello, " + name appends the value of name to the hello string, which creates a personalized greeting

Since addition is defined for both numbers and strings, Java performs automatic conversions you may not expect:

What do we expect the following code to print?

String s = "Hello";
System.out.println(1 + 2 + s);

How about this one?

System.out.println(s + 1 + 2);

Java executes these operations from left to right.

• In the first example, 1 + 2 is 3, and 3 + the value of variable s ("Hello") is "3Hello"


• In the second example, "Hello" + 1 is "Hello1", and "Hello1" + 2 is "Hello12"

The System class also provides the special value System.in, which is an InputStream that provides methods for reading input from the keyboard. These methods are not easy to use; fortunately, Java provides other classes that make it easier to handle common input tasks.

All reading done in Java uses the Scanner class. Using this class, we can create an object to read input from the standard input channel System.in (in our case, the keyboard)

To use the Scanner class, it is necessary to import the class Scanner from the library java.util by including the following line at the top (before the class declaration) of program:

import java.util.Scanner;

We can declare a Scanner object by saying:

Scanner sc = new Scanner (System.in);

• sc is the name of the Scanner object (this can be changed and is entirely up to the person who writes the code)
• and System.in connects our object to standard input (the keyboard)

The Scanner class has multiple built-in methods that we can access to help us read data, for example: we can use sc.nextLine() to read in a line of String(s) (spaces included)

Other methods include:

• nextBoolean(): reads a boolean value from the user
• nextByte(): reads a byte value from the user
• nextDouble(): reads a double value from the user
• nextFloat(): reads a float value from the user
• nextInt(): reads a int value from the user
• next(): reads a complete token (String) from the user. A complete token is preceded and followed by input that matches the delimiter pattern, in most instances this is a space

When we are done reading in data, it is customary to CLOSE the Scanner to avoid a possible memory leak. This is simple, we would just state thr following:

sc.close();

Once we no longer need the Scanner (this is typically found at the last could lines of the method)

Now that we have had some experience with Scanner, we need to talk about some unexpected behavior that may occur

When you read a String followed by an int, everything works just fine.But when you read an int followed by a String, something strange happens.

System.out.print("What is your age? ");
age = in.nextInt();
System.out.print("What is your name? ");
name = in.nextLine();
System.out.printf("Hello %s, age %d\n", name, age);

Try running this example code. It doesn't let you input your name, and it immediately displays the output:

What is your name? Hello , age 45

When you call nextInt(), it reads characters until it gets to a non-digit. At this point, nextInt() returns 45. The program then displays the prompt "What is your name? " and calls nextLine(), which reads characters until it gets to a newline. But since the next character is already a newline, nextLine returns the empty string "".

To solve this problem, you need an extra nextLine() after nextInt()

System.out.print("What is your age? ");
age = in.nextInt();
in.nextLine();// read the newline
System.out.print("What is your name? ");
name = in.nextLine();
System.out.printf("Hello %s, age %d\n", name, age);

This technique is common when reading int or double values that appear on their own line.

First you read the number, and then you read the rest of the line, which is just a newline character.

Now let's see an example, We will use a Scanner to input a measurement in inches, convert to centimeters, and then display the results.

First let's declare the variables and create the Scanner object that we will call input

int inches;
double cm;
Scanner input = new Scanner(System.in);

Next, let's prompt the user for the input (prompts are important because they let the user know HOW they should interact with the program)

We'll use print() instead of println() so they can enter the input on the same line as the prompt and use the Scanner method nextInt(), which reads input from the keyboard and converts it to an integer

System.out.print("Enter # of inches: ");
inches = input.nextInt();

Now we can multiply the number of inches entered by 2.54 (the number of centimeters there are per inch) and display the results

cm = inches * 2.54;
System.out.print(inches + " inches = ");
System.out.printf("%.2f cm%n", cm);

This code works but it does have a minor flaw. If another programmer reads this code, they might wonder where 2.54 comes from.

How can we modify this for clarity?

A value that appears in a program, like 2.54 (or " inches = "), is called a literal.

In general, there is nothing wrong with literals.

But when numbers like 2.54 appear in an expression with no explanation, they make code hard to read. And if the same value appears many times, and might have to change in the future, it makes code hard to maintain.

For the benefit of others (and yourself in the future), it would be better to assign this value to a variable with a meaningful name:

double cmPerInch = 2.54;
cm = inches * cmPerInch;

This version is easier to read and less error-prone, but it still has a problem. Variables can vary, but the number of centimeters in an inch does not.

Once we assign a value to cmPerInch, it should never change.

Luckily, Java provides a language feature that enforces that rule, the keyword final.

final double CM_PER_INCH = 2.54;

Declaring a variable as final means that it cannot be reassigned once it has been initialized. If you try, the compiler reports an error.

Variables declared as final are called constants.

• By convention, names for constants are all uppercase, with the underscore character (_) between words.

At this point, we have now seen enough Java to write useful programs that solve everyday problems.

We can:

1. import Java library classes
2. create a Scanner
3. get input from the keyboard
4. complete any necessary calculations
5. print and format output to the screen

At this point, we have seen all of the elements that make up Java programs.

Figure 3.2 shows these organizational units.

As previously mentioned, we use a Scanner to read data whether or not the data is from the keyboard or a file. To read from a file we only need to make one or two modifications from what we learned from reading from the keyboard.

First, since we are using files we need to allow our program(s) to use them by including:

import java.io.File;//import the File class

Since we are dealing with files, we HAVE to add a throws Exception declaration to main:

public static void main (String [] args) throws Exception {

and create the File object that we will be reading from:

File file = new File("[filename].txt");

And create a Scanner like we have previously done, only changing our reference from the keyboard to the corresponding file object:

Scanner sc = new Scanner(file);

• It is important that you remember to create the .txt file that you are trying to reading from and make sure that it is in the correct directory or to specify the path where the file is located when creating the File object else you will receive a FileNotFoundException when you attempt to run your code.

We already know about writing data to the screen by using System.out, but how about writing data to an outside source such as a file?

Writing to a file is slightly less work since we do not have to manually create the .txt file ourselves prior to running the program, the program will do the creation for us. There are many different ways to write to file in Java but in this class we will keep it relatively simple and use the PrintWriter class.

Like before, we need to import the PrintWriter class in order to use it:

import java.io.PrintWriter;

Whether we are writing or reading, we are still dealing with files so we still HAVE to add a throws Exception declaration to main:

public static void main (String [] args) throws Exception {

and create the File object that we will be reading from:

We will use the PrintWriter class to create our file:

PrintWriter pw = new PrintWriter("[filename].txt");

• It is important to make sure that the filename that you are trying to create does not already exist in the directory that you are trying to create it in otherwise, you will overwrite the file and lose your original file data

Now we can use the PrintWriter object to write, the same way that we wrote to the screen only replacing System.out with our PrintWriter object, i.e. pw.print(), pw.println(), pw.printf(), etc.

Just like with the Scanner, we need to CLOSE the PrintWriter object:

pw.close();

The intepreter only knows that the program is finished writing to the file after we close the PrintWriter, so if we forget to close the PrintWriter the file may appear empty.

Importantly, .close() automatically flushes the stream before closing it, meaning any data remaining in the buffer will be written to the output.

So far we have seen programs that do pretty much the same thing every time, regardless of the input. For more complex computations, programs usually react to the inputs, check for certain conditions, and generate appropriate results.

We mentioned relational operators briefly before but let's discuss how they work, more in depth:

Relational operators are used to check conditions like whether two values are equal, or whether one is greater than the other.

You have probably seen these operations before, but it is important to note that the Java operators are different from the mathematical symbols like =, ≠, and ≤.

A common error is to use a single = instead of a double ==

Remember that:

• = is the assignment operator
• and == is a comparison operator

The two sides of a relational operator must be compatible

For example, the expression: 5 < "6" is invalid because 5 is an int and "6" is a String

However, when evaluating the expression 5 (an int) < 6.0 (a double), Java automatically converts the 5 to 5.0 because when comparing values of different numeric types, Java applies the same conversion rules we saw previously with the assignment operator.

The result of a relational operator is one of two special values, either true or false.

These values belong to the data type boolean. In fact, they are the only boolean values.

The results of these operators are similar to their meanings in English.

For example:

• (x > 0 && x < 10) is true when x is both greater than zero and less than 10
• The expression (evenFlag || n % 3 == 0) is true if either condition is true, that is, if evenFlag is true or the number n is divisible by 3
• And the ! operator inverts a boolean expression, so !evenFlag is true if evenFlag is not true (false)

Logical operators evaluate the second expression only when necessary. For example:

• (true || anything) is always true, so Java does not need to evaluate the expression anything
• and (false && anything) is always false

Ignoring the second operand, when possible, is called short circuit evaluation, by analogy with an electrical circuit.

Short circuit evaluation can save time, especially if anything takes a long time to evaluate. It can also avoid unnecessary errors, if anything might fail.

If I told you I would show you a picture of a blue square and then you saw the picture and it wasn't true, which part of my claim “a blue square” wasn't true?

Maybe it was a square and it was a color other than blue? Or maybe it wasn't even a square at all? Maybe it was neither blue NOR a square entirely?

You could write this as a logic statement like below using negation (!) and the AND (&&) operator since both parts have to be true for the whole statement to be true.

If you ever have to negate an expression that contains logical operators, and you probably will, De Morgan's laws can help.

De Morgan's Laws were developed by Augustus De Morgan in the 1800s. They show how to simplify the negation of a complex boolean expression, which is when there are multiple expressions joined by an AND (&&) or OR (||), such as
(x < 3) && (y> 2).

Negating a logical expression is the same as negating each term and changing the operator. The ! operator takes precedence over && and ||, so you don't have to put parentheses around the individual terms !A and !B.

Here's an easy way to remember De Morgan's Laws:

• move the NOT inside, AND becomes OR
• and move the NOT inside, OR becomes AND

In Java, De Morgan's Laws are written with the following operators:

• !(a && b) is equivalent to !a || !b
• !(a || b) is equivalent to !a && !b

Going back to our example above, using De Morgan's Laws:

• !("blue" && "square") is equivalent to !("blue") or !("square")

You can also simplify negated boolean expressions that have relational operators like <,>, ==. You can remove negation by moving it inside and flipping the relational operator to its opposite sign.

For example, (!) not (c equals d) is the same as saying c does not equal d.

An easy way to remember this is to:

• Move the NOT inside, flip the sign
• i.e. == becomes !=, < becomes>=, and > becomes <=< /b>

In this case, negating each term means using the “opposite” relational operator. For example:

• !(x < 5 && y==3) is the same as x >= 5 || y != 3
• !(x >= 1 || y != 7) is the same as x < 1 && y==7

It may help to read these examples out loud in English. For instance, "If I don't want the case where x is less than 5 and y is 3, then I need x to be greater than or equal to 5, or I need y to be anything but 3."

You should be able to show that two boolean expressions are equivalent. One way to do this is by using truth tables.

For example, we can show that !(a && b) == !a || !b by constructing the truth table below and seeing that they give identical results for the 2 expressions (the last 2 columns in the table below are identical!):

a	b	!(a && b)	!a || !b
true	true	false	false
false	true	true	true
true	false	true	true
false	false	true	true

Often, you can simplify boolean expressions to create equivalent expressions.

For example, applying De Morgan's Laws to !(x < 3 && y> 2) yields !(x < 3) || !(y> 2) as seen in the figure below.

This can then be simplified further by moving the not operator inside and flipping the relation operators. So, !(x < 3) || !(y> 2) is simplified to (x >= 3 || y <= 2) where the relational operators are flipped and the negation is removed. These two simplification steps are seen below.

char choice = sc.next().charAt(0);

The .charAt() method returns the character at the specified index in a String and the index of the first character is 0 (we will talk more about the other characters when we talk more about Strings and their methods)

Doing this is a loophole to read in char values from the keyboard.

Programs are often used to automate repetitive tasks. Running the same code multiple times is called iteration.

Java provides language features that make iteration easy: loops such as the while loop, the do-while loop, and the for loop.

In programming, loops are important to learn and understand how to use to be able to create dynamic programs that can do a lot of different things.

Loops are a programming element that repeat a portion of code a set number of times until the desired process is complete. Repetitive tasks are common in programming, and loops are essential to save time and minimize errors.

Think about HW 1 and part 1 of HW 2: we processed the required medical dosage for a set of patients.

Each patient's dosage is calculated EXACTLY the same way:

• First by reading in the patient's weight,
• Then by converting the weight from pounds (lbs) to kilograms (kg),
• Lastly, we multiply the weight in kilograms by 30 since each kilogram of weight requires a dosage of 30 milligrams (mg)

Instead of rewriting the block of code for each new patient, we can implement a loop!

When programmers write code, loops allow them to shorten what could be hundreds of lines of code to just a few.

This allows them to write the code once and repeat it as many times as needed, making it more likely for the program to run as expected (less chance of error).

A while loop is a control flow statement that allows code to be executed repeatedly based on a given boolean condition.

The while loop can be thought of as a repeating if statement.

The expression in parentheses is called the condition. The statements in braces are called the body. The flow of execution for a while statement is:

1. Evaluate the condition, yielding true or false.
2. If the condition is false, skip the body and go to the next statement.
3. If the condition is true, execute the body and go back to step 1.

This type of flow is called a loop, because the last step loops back around to the first.

You may find that the breakdown of the while loop sounds quite similar to the parts that make up the if statement that we previous discussed. And you would be right!

There are similarities in the structure of both concepts, however, there are a significant differences as well.

An if statement, when true, will only execute the inner block of code once.

In contrast, a while loop will continue to execute the inner block of code as long as the condition is true.

If the condition is initially false (in either case), the inner block of code will never execute.

The body of the loop should change the value of one or more variables so that, eventually, the condition becomes false and the loop terminates.

The termination is important, otherwise the loop will repeat forever, which is called an infinite loop.

An endless source of amusement for computer scientists is the observation that the directions on shampoo, “Lather, rinse, repeat,” are an infinite loop.

For example, we can write a simple loop to act as a countdown:

int n = 10;
while (n > 0) {
    System.out.println(n);
    n = n - 1;
}
System.out.println("Blastoff!");

You can almost read the while statement like English:

"While n is greater than zero, print the value of n and then reduce the value of n by 1. When you get to zero, print Blastoff!"

In this case, the loop terminates when n is no longer positive. But in general, it is not so easy to tell whether a loop terminates.

The Collatz conjecture is one of the most famous unsolved problems in mathematics, named after Lothar Collatz. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1.

The problem is stated as follows:

• Start with any positive integer n
• If n is even, the next number is n/2
• If n is odd, the next number is 3n+1

The conjecture is that these sequences always reach 1 (more specifically ends in the values 4, 2, 1), no matter which positive integer is chosen to start the sequence.

import java.util.Scanner;

public class CollatzConjecture {
    public static void main(String [] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("Enter a posititve Integer: ");
        int x = sc.nextInt();
        System.out.println(x);
        while (x != 1) { //until x is equal to 1
            if (x % 2 == 0) { //x is even
                x = x / 2;
                System.out.println(x);
            } else { //x is odd
                x = 3 * x + 1;
                System.out.println(x);
            }
        }
    }          
}

Each time through the loop, the program displays the value of x and then checks whether it is even or odd.

If it is even, the value of x is divided by two.

If it is odd, the value is replaced by 3x + 1.

For example, if the starting value (the argument passed to sequence) is 3, the resulting sequence is 3, 10, 5, 16, 8, 4, 2, 1.

Since x sometimes increases and sometimes decreases, there is no obvious proof that x will ever reach 1 and that the program will ever terminate.

However, the rules of Collatz Conjecture lets us know that it will.

The hard question is whether this program terminates for all values of x. So far, no one has been able to prove it or disprove it!

Loops are good for generating and displaying tabular data.

The following code starts with an integer n and then use a loop to display a multiplication table with a sequence of values (n*1, n*2, ... etc.) in the left column and the results in the right column (after the equal sign):

Let's trace it!

int n = 9; 
int i = 1;
while(i <= 10) {
    System.out.printf("%d * %d = %d \n", n, i, n * i);
    i++;
}

Sometimes, we know in advance how many times we want to do something, i.e.:

• do this ten times
• do this five times
• pick a random number, and do it that many times

We can do that sort of thing with a while loop, but we have to use a counter.

A counter variable in Java is a special type of variable which is used in the loop to count the repetitions or to know about in which repetition we are in.

In simple words, a counter variable is a variable that keeps track of the number of times a specific piece of code is executed.

The counter variable is declared and used in the same way as the normal variables are declared and used.

The counter variable can be of only integer type because it is very easy to increase the value of integer type variable.

The counter variable is very easy to understand and use. The technique of using the counter variable in Java is as follows:

Before the repeating cycle, we have to initialize it to zero.

After that, we're going to be adding 1 to the counter everytime we repeat the loop. And when the counter reaches a predetermined value, we'll stop looping.

Let's take a simple example to understand the concept of the counter variable in Java:

int count = 0;// count is initialized
while (count <= 10) {// count is tested
    System.out.print(count + " ");
    count++;// count is incremented, increased by 1
}

The first statement in the loop prints value of count.

The second statement uses the increment operator to add one to number.

After it executes, the loop starts over. It tests the boolean expression again.

If it is true, the statements in the body of the loop are executed.

This cycle repeats until the boolean expression number <= 10 is false.

The loop in above example is controlled by a counter, so it is known as a counter controlled loop.

However, while loops are best for repeating as long as something is true:

• keep going as long as they keep typing in a positive number
• keep going as long as they haven't typed in a zero

The loop in next example is a sentinel controlled loop, a special value (the "sentinel") that is used to signify when the loop is done.

public static void main(String [] args) {
    int sum = 0;// initialize the sum
    int count = 0;//initialize counter
    //create a Scanner object for keyboard input.
    Scanner sc = new Scanner(System.in);
      
    //get the first value.
    System.out.print("Enter first integer (enter 0 to quit): ");
    int value = sc.nextInt();
      
    while (value != 0) {
        count++;//increment count for each value
        sum = sum + value;//add value to sum
      
        //get next value from the user to avoid infinite loop!
        System.out.print("Enter next integer (enter 0 to quit): ");
        value = sc.nextInt();
    }
      
    //display the total sum and count
    System.out.println("Sum of the integers: " + sum);
    System.out.println("Total integers entered: " + count);
}

Here the loop allows the user to keep entering numbers (and adding the entered numbers to the running sum and counting how many numbers are entered) UNTIL the user enters a zero.

Now that we know a bit about iteration, let's discuss the different types:

A pretest loop tests its condition before each iteration.

Examples include:

• while loops
• for loops

A posttest loop tests its condition after each iteration.
A posttest loop will always execute at least once.

Examples include:

• do/while loops

This type of loop is useful when you need to run the body of the loop at least once.

The do-while loop is a variant of the while loop.

It is very similar to the while loop with one distinct difference.

So let's discuss the specific behavior that separates them from each other:

• As previously discussed, the while loop checks the condition first, and if it returns true, the code within it runs. The loop continues until the condition provided returns false, then stops.



• Alternatively, the do-while loop runs its code once before checking the condition and runs again only if the condition is true. This continues until the condition check returns false, then it stops before the next loop starts.

The loop will always be executed at least once, even if the condition is false, because the code block is executed before the condition is tested.

The execution of do-while loop is as follows:

1. Enter the do-while loop
2. The statements inside the body of the loop get executed
3. Any updation takes place
4. The flow jumps to Condition
5. The Condition is tested
1. If Condition yields true, go to Step 6
2. If Condition yields false, the flow goes outside the loop
6. The flow goes back to Step 2

As aforementioned, the do-while loop is useful for when you want to execute something at least once.

As for a good example for using do-while vs. while, lets say we want to modify our previous Medical Dosage Calculator.

We could approach this by using a while loop and checking after each calculation if the person wants to exit the program (as we discussed last class)

public static void main(String [] args) {
    final double LBS_TO_KG = 0.45359237;
    final double DOSE_PER_KG = 30;
    Scanner sc = new Scanner(System.in);
    //create count to keep track of # of patients
    int count = 0;
    //prompt user to interact
    System.out.print("Would you like to enter a patient? (Y/N):");
    //identify new patient Y/N?
    char op = sc.next().charAt(0);//reads in Y or N
    
    while (op != 'N' && op != 'n') {
        System.out.print("Enter patient's weight: ");
        double weight = sc.nextDouble();
        double kilo = weight * LBS_TO_KG;
        double dosage = kilo * DOSE_PER_KG;
        count++;
        System.out.printf("Dosage required for Patient %d is: %.2f%n%n", 
                            count, dosage);
        //prompt user to interact
        System.out.print("Would you like to enter another patient? (Y/N): ");
        //identify new patient Y/N?
        op = sc.next().charAt(0);//reads in Y or N
    }
    
    System.out.printf("%nTotal number of patients processed: %d%n", count);
    
}

Now we can probably assume that once the program is opened the user wants to interact with it at least once so we could modify our code to use a do-while loop.

We have already seen the break statement used earlier, it was used to "jump out" of a switch statement.

The break statement can also be used to jump out of a loop.

The following example stops the loop when i is equal to 4 despite the original condition of the while loop:

int i = 0;
while (i < 10) {
    System.out.println(i);
    i++;
    if (i == 4) {
        break;
    }  
}

The continue statement breaks one iteration (in the loop), if a specified condition occurs, and continues with the next iteration in the loop

The following example skips the value of 4:

int i = 0;
while (i < 10) {
    if (i == 4) {
        i++;//why do we need to do this? 
        continue;
    }
    System.out.println(i);
    i++; 
}

For example, we can use a do-while loop to keep reading input until it's valid:

Scanner in = new Scanner(System.in);
boolean okay;
do {
    System.out.print("Enter a number: ");
    if (in.hasNextDouble()) {
        okay = true;
    } else {
        okay = false;
        String word = in.next();
        System.out.println(word + " is not a number");
    }
} while (!okay);
double x = in.nextDouble();
System.out.println("\nYou entered the number: " + x);

Although this code looks complicated, it is essentially only three steps:

1. Display a prompt
2. Check the input; if invalid, display an error and start over
3. Read the input

The code uses a flag variable, okay, to indicate whether we need to repeat the loop body.

If .hasNextDouble() returns false, we consume the invalid input by calling .next(). We then display an error message.

The loop terminates when .hasNextDouble() returns true.

A simpler way to solve this problem is to use a break statement.

Scanner in = new Scanner(System.in);
while (true) {
    System.out.print("Enter a number: ");
    if (in.hasNextDouble()) {
        break;
    } else {
        String word = in.next();
        System.out.println(word + " is not a number");
    }
}
double x = in.nextDouble();
System.out.println("\nYou entered the number: " + x);

Using true as a conditional in a while loop is an idiom that means "loop forever", or in this case "loop until you get to a break statement".

Although break and continue statements give you more control of the loop execution, they can make code difficult to understand and debug.

Use them sparingly.

The loops we have written so far have several elements in common.

They start by:

• initializing a variable
• they have a condition that depends on that variable
• and inside the loop they do something to update that variable

When we know exactly how many times we want to loop through a block of code, we use the for loop instead of a while loop.

Unlike the while and do/while loops, the for loop has all three components enclosed in the parentheses, separated by semicolons: the initializer, the condition, and the update.

1. The initializer runs once at the very beginning of the loop
2. The condition is checked each time through the loop
• If it is false, the loop ends
• Otherwise, the body of the loop is executed (again)
3. At the end of each iteration, the update runs, and we go back to step 2

The for loop is often easier to read because it puts all the loop-related statements at the top of the loop.

How does the for loop work?

1. Control falls into the for loop, initialization is done
2. The flow jumps to the Condition
3. Condition is tested
• If the Condition is true, the flow goes into the body of the loop
• If the Condition is false, the flow goes outside the loop
4. (If true) The statements inside the body of the loop get executed.
5. The flow goes to the Updation
6. Updation (the variable is updated) takes place and the flow goes to Step 3 again
7. (If false) The for loop has ended and the flow has gone outside of the loop

The example below will print the numbers 0 to 4 (inclusive):

for (int i = 0; i < 5; i++) {
    System.out.println(i);
}

• The first statement in the parentheses, initializes a variable before the loop starts (int i = 0)
• The second defines the condition for the loop to run (i must be less than 5)
• If the condition is true, the loop will start over again
• If it is false, the loop will end
• The last part enclosed in the parentheses increases a value (i++) each time the code block in the loop has been executed

There is one difference between for loops and while loops: if you declare a variable in the initializer, it only exists inside the scope of the for loop.

For example, if we attempted to print out the value of i after the loop we would get an error:

for (int i = 0; i < 5; i++) {
    System.out.println(i);
}
System.out.println(i); // compiler error

The last line tries to display i (for no reason other than demonstration) but it won't work. If you need to use a loop variable outside the loop, you have to declare it outside the loop, like this:

int i;
for (i = 0; i < 5; i++) {
    System.out.println(i);
}
System.out.println(i);

Assignments like i = i + 1 don't often appear in for loops, because Java provides a more concise way to add and subtract by one.

Specifically, ++ is the increment operator; it has the same effect as i = i + 1.

And -- is the decrement operator; it has the same effect as i = i - 1.

If you want to increment or decrement a variable by an amount other than 1, you can use += and -=. For example, i += 2 increments i by 2.

This example will only print even values between 0 and 10 (inclusive):

for (int i = 0; i <= 10; i += 2) {
    System.out.println(i);
}

How can we rewrite this so that it iterates over every number (not just the even ones) but only prints out the even numbers (that way the output will be the same as the previous code)? (Hint: use an if statement)

If a loop exists inside the body of another loop, it's called a nested loop. Here's an example of the nested for loop:

for (int i = 1; i <= 2; i++) {// Outer loop
    System.out.println("Outer: " + i);// Executes 2 times
    
    for (int j = 1; j <= 3; j++) {// Inner loop
        System.out.println(" Inner: " + j);// Executes 6 times (2 * 3)
    }
}

The inner loop will be re-executed for each iteration of the outer loop.

Example: We can use the nested loop to iterate through each day of a week for 4 weeks (a month).

In this case, we can create a loop to iterate four times (4 weeks). And, inside the loop, we can create another loop to iterate 7 times (7 days).

public static void main(String [] args) {
    int weeks = 4;//4 weeks in a month (on average)
    int days = 7;// 7 days in a week
      
    // outer loop prints weeks
    for (int i = 1; i <= weeks; i++) {
        System.out.println("Week: " + i);
      
        // inner loop prints days
        for (int j = 1; j <= days; j++) {
            System.out.println("  Day: " + j);
        }
        System.out.println();//skip a line for every new week
    }
}

Alternate: for loop inside the while loop

We can write the same exact program only using a while loop as the outer loop instead. The following code shows how:

int weeks = 4;
int days = 7;
int i = 1;//necessary for outer loop

// outer loop prints weeks
while (i <= weeks) {
    System.out.println("Week: " + i);

    // inner loop
    for (int j = 1; j <= days; j++) {
        System.out.println("  Days: " + j);
    }
    i++;//NEED TO INCREMENT
}

We can see that the output of both examples are the same.

Example: Nested loops to create a pattern

We can use the nested loop in Java to create patterns like full pyramid, half pyramid, inverted pyramid, and so on.

Here is a program to create a half pyramid pattern using nested loops:

public static void main(String [] args) {
    int rows = 5;
    
    // outer loop
    for (int i = 1; i <= rows; ++i) {
    
        // inner loop to print the numbers
        for (int j = 1; j <= i; ++j) {
            System.out.print(j + " ");
        }
        System.out.println();
    }
}

There are several differences among the three types of loops in Java, such as the syntax, optimal time to use, condition checking, and so on. The table below represents some of the primary dissimilarities between all the loops in Java.

We have learned a bit about characters before (see: The char Data Type) as another means of choice input, however, they can be used for so much more!

But first, what are characters anyway?

We can think of a char in Java as a single letter in a word – it represents a single character, and it's a fundamental part of Java programming.

To declare and use a char in Java, you use the char keyword before a variable name.

We can then manipulate and use this char in various ways in our programs.

char letter = 'A';
System.out.println(letter);

In the above example, we declare a char variable named letter and assign it the value 'A'. We then print out the value of letter, which outputs 'A'.

Character literals, like 'a', appear in single quotes. Unlike string literals, which appear in double quotes (""), character literals can only contain a single character. Escape sequences, like '\t' or '\n', are legal because they represent a single character.

This is a key difference between chars and strings in Java.

Chars are incredibly efficient in terms of memory usage. Each char in Java takes up only 2 bytes of memory, making them a great choice when memory usage is a concern.

However, as previously mentioned, chars in Java can represent a single character only. If we need to work with multiple characters, we will need to use a string or an array of chars (we'll talk about this more in a bit).

Also, remember that chars in Java are case-sensitive. This means that the char 'a' is different from the char 'A'. Always be mindful of this when working with chars in Java.

As you become more familiar with Java char, you'll find that there's a lot more you can do beyond simply declaring and printing them. Let's delve into some of these advanced techniques, such as manipulating and comparing characters.

We can perform arithmetic operations on chars in Java, similarly to ints and doubles. This is because chars in Java are, in fact, numeric values representing Unicode characters.

The increment and decrement operators work perfectly normal with characters.

Here is an example:

char letter = 'A';
letter++;
System.out.println(letter);

In the above example, we increment the char 'A' by 1, which results in the char 'B'.

This is because in the Unicode character set, 'B' is one position after 'A'.

The character 'A' has a Unicode value of 65, so adding 1 to it results in the Unicode value of 66 or most notably the char 'B'.

We can do the same with the other arithmetic operations as well! For example, subtraction:

char letter = 'W';
letter--;
System.out.println(letter); //What will this print out?

We can also use chars in loops, the following loop displays the letters of the alphabet:

System.out.print("English alphabet: ");
for (char c = 'A'; c <= 'Z'; c++) {
    System.out.print(c + " ");
}
System.out.println();

Just like with int or double we can also cast a number to a char using typecasting. (once again, see: The char Data Type)

Characters work like the other primitive types we have seen. You can compare them using relational operators:

char firstLetter = 'A';
char secondLetter = 'B';
System.out.println(firstLetter < secondLetter); //(T or F)

In this code snippet, we compare two chars 'A' and 'B'. Since 'A' comes before 'B' in the Unicode character set, the expression 'firstLetter < secondLetter' returns true.

Since, we can use relational operators with chars we can also use them in boolean conditions such as the following:

if (firstLetter == 'A') {
    System.out.println("The first letter is " + firstLetter);
}

While the char data type is a powerful tool for handling single characters in Java, there are alternative approaches that offer additional functionality. We will explore two of these: the Character wrapper class and using Strings.

Most of the time, if you are using a single character value, you will use the primitive char type.

However in programming, we come across situations where we need to use objects instead of primitive data types. In order to achieve this, Java provides wrapper class Character for primitive data type char.

Character is a wrapper class that "wraps" the char in a Character object.

An object of type Character contains a single field, whose type is char. You can create a Character object with the Character constructor.

To create a Character object:

Character ch = new Character('A');

The above statement creates a Character object which contains 'A' of type char.

This Character class also offers a number of useful class (that is, static) methods for manipulating characters.

The following table lists some of the most useful methods in the Character class:

For a complete listing of all methods in this class (there are more than 50), refer to the java.lang.Character API specification.

Here is an example of using the Character class to convert a char to uppercase:

char lowercaseLetter = 'a';
char uppercaseLetter = Character.toUpperCase(lowercaseLetter);
System.out.println(uppercaseLetter);

In this example, we use the .toUpperCase() method of the Character class to convert the lowercase char 'a' to an uppercase 'A'.

Strings are the type of objects that can store the character of values and in Java.

A String class object acts the same as an array of characters in Java.

In Java, objects of the String class are immutable which means that they are constant and cannot be changed once created.

A String variable contains a collection of characters surrounded by double quotes:

String greeting = "Hello!";

A String in Java is actually an object, which means that it contains methods that can perform certain operations on Strings.

A couple of the methods, toUpperCase() and toLowerCase() convert from uppercase to lowercase and back. These methods are often a source of confusion, because it sounds like they modify strings. But neither these methods nor any others can change a string, because strings are immutable

When you invoke toUpperCase() on a string, you get a new string object as a return value. For example:

String name = "Alan Turing";
String upperName = name.toUpperCase();

After these statements run, upperName refers to the String "ALAN TURING". But name still refers to "Alan Turing".

Another useful method is replace(), which finds and replaces instances of one String within another. This example replaces "Computer Science" with "CS":

String text = "Computer Science is fun!";
text = text.replace("Computer Science", "CS");

This example demonstrates a common way to work with String methods.

It invokes text.replace(), which returns a reference to a new String: "CS is fun!". Then it assigns the new string to text, replacing the old String.

This assignment is important; if you don’t save the return value, invoking text.replace() has no effect.

Strings provide a method called length() that returns the number of characters in the string.

For example:

String fruit = "banana";
System.out.println("The length of the String is: " + fruit.length());

The Java String class charAt() method returns a char value at the given index number.

Since a String is technically an array of characters, the index number starts from 0 and goes to n-1, where n is the length of the string.

char ch = fruit.charAt(2);//returns the char value at the 2nd index  
System.out.println(ch);

To find the last letter of a string, you might be tempted to try something like:

int length = fruit.length();
char last = fruit.charAt(length);//wrong!

This code compiles and runs, but invoking the charAt method throws a StringIndexOutOfBoundsException.

The problem is that there is no letter at the sixth index in "banana". Since we started counting at 0, the 6 letters are indexed from 0 to 5.

To get the last character, you have to subtract 1 from length.

int length = fruit.length();
char last = fruit.charAt(length - 1);//correct!

Many String traversals involve reading one String and creating another. For example, to reverse a String, we simply add one character at a time:

String reverse = "";
for (int i = fruit.length() - 1; i >= 0; i--) {
    reverse = reverse + fruit.charAt(i);
}
System.out.println(reverse);

The initial value of reverse is "", which is the empty String.

The loop traverses the letters of fruit in reverse order. Each time through the loop, it creates a new String and assigns it to reverse. When the loop exits, reverse contains the letters from fruit in reverse order.

So the result of when fruit is "banana" is "ananab".

The .substring() method returns a new string that copies letters from an existing string, starting at the given index.

For example:

• fruit.substring(0) returns "banana"
• fruit.substring(2) returns "nana"
• fruit.substring(6) returns ""

The first example returns a copy of the entire String. The second example returns all but the first two characters. As the last example shows, substring returns the empty String if the argument is the length of the String.

To visualize how the substring method works, it helps to draw a picture like the following:

Like most String methods, .substring() is overloaded. That is, there are other versions of .substring() that have different parameters. If it's invoked with two arguments, they are treated as a start and end index:

• fruit.substring(0, 3) returns "ban"
• fruit.substring(2, 5) returns "nan"
• fruit.substring(6, 6) returns ""

Notice that the character indicated by the end index is not included. Defining .substring() this way simplifies some common operations.

For example, to select a .substring() with length len, starting at index i, you could write fruit.substring(i, i + len).

The .indexOf() method searches for a character in a String.

There are four variants of the .indexOf() method:

• int indexOf()


• This method returns the index within this string of the first occurrence of the specified character or -1, if the character does not occur.


• int indexOf(char ch, int strt)


• This method returns the index within this string of the first occurrence of the specified character, starting the search at the specified index or -1, if the character does not occur.


• int indexOf(String str)


• This method returns the index within this string of the first occurrence of the specified substring. If it does not occur as a substring, -1 is returned.


• int indexOf(String str, int strt)


• This method returns the index within this string of the first occurrence of the specified substring, starting at the specified index. If it does not occur, -1 is returned.

This example finds the index of 'a' in the String:

String fruit = "banana";
int index = fruit.indexOf('a');

But the letter appears three times, so it's not obvious what .indexOf() should do.

According to the documentation, it returns the index of the first appearance.

To find subsequent appearances, you can use the second version of .indexOf(), which takes a second argument that indicates where in the String to start looking.

int index = fruit.indexOf('a', 2);

This code starts at index 2 (the first 'n') and finds the next 'a', which is at index 3. If the letter happens to appear at the starting index, the starting index is the answer. So fruit.indexOf('a', 5) returns 5.

We can also find the last occurrence of a character. The .lastIndexOf() method returns the position of the last occurrence of specified character(s) in a String.

Like .indexOf(), there are four variants of the .lastIndexOf() method:

To compare two Strings, it may be tempting to use the == and != operators.

String name1 = "Alan Turing";
String name2 = "Ada Lovelace";
if (name1 == name2) { // wrong!
    System.out.println("The names are the same.");
}

This code compiles and runs, and most of the time it gets the answer right. But it is not correct, and sometimes it gets the answer wrong.

The problem is that the == operator checks whether the two variables refer to the same object (by comparing the references). If you give it two different Strings that contain the same letters, it yields false.

The right way to compare Strings is with the equals method, like this:

if (name1.equals(name2)) {
    System.out.println("The names are the same.");
}

This example invokes equals on name1 and passes name2 as an argument. The equals method returns true if the strings contain the same characters; otherwise it returns false.

If the Strings differ, we can use the .compareTo() method to see which comes first in alphabetical order:

int diff = name1.compareTo(name2);
if (diff == 0) {
    System.out.println("The names are the same.");
} else if (diff < 0) {
    System.out.println("name1 comes before name2.");
} else if (diff > 0) {
    System.out.println("name2 comes before name1.");
}

The return value from .compareTo() is the difference between the first characters in the strings that differ.

• If the Strings are equal, their difference is zero.
• If the first String (the one on which the method is invoked) comes first in the alphabet, the difference is negative.
• Otherwise, the difference is positive.

In the preceding code, compareTo returns positive 8, because the second letter of "Ada" comes before the second letter of "Alan" by 8 letters.

Both .equals() and .compareTo() are case-sensitive. The uppercase letters come before the lowercase letters, so "Ada" comes before "ada".

The .equalsIgnoreCase() method compares two Strings, ignoring lower case and upper case differences. This method returns true if the Strings are equal, and false if not.

Use the .compareToIgnoreCase() method to compare two Strings lexicographically, ignoring case differences.

We previously learned how to use .printf() to display formatted output. Sometimes programs need to create Strings that are formatted a certain way, but not display them immediately, or ever.

In Java, the String.format() method returns a formatted string using the given locale, specified format String, and arguments. We can concatenate the Strings using this method and at the same time, we can format the output concatenated String.

String.format() takes the same arguments as System.out.printf(): a format specifier followed by a sequence of values.

The main difference is that while System.out.printf() displays the result on the screen, String.format() creates a new String, but does not display anything.

The String .split() method breaks a String around matches of the given regular expression (regex). After splitting against the given regular expression, this method returns a String array.

Regex characters are either metacharacters or regular characters. Metacharacters have a specific meaning.

In regex, the period "." is a metacharacter that stands in for any character. We can use ".." in regex to represent a pattern of any two characters. It could be "aa", "!2", "y)" or any other combination.

If we want to search specifically for let's say a filename that ends in “.rb” we could use "r" and "b" as is because they are regular characters which have a literal meaning.

To get the period we have to use a backslash in front to make it an escaped character. Since regexes in Java are normal Java strings, we need to escape the backslash itself, so we need two backslashes e.g. \\.

Example:

public static void main(String [] args) {
    String text = "Java is a fun programming language";   
    // split string from space
    String [] result = text.split(" ");
                                
    System.out.print("result = ");
    for (String str : result) {
        System.out.print(str + ", ");
    }
}

Another Example:

public static void main(String [] args) {
    String str = "Let's:split:another:String";
    String [] arrOfStr = str.split(":");
    for (String a : arrOfStr) { //enhanced for loop
        System.out.println(a);
    }
}

In the example above, we use : as the delimiter, so the original String is split into an array of individual Strings separated by the colon (:).

Let's split on a period:

public static void main(String [] args) {
    String str = "Let's.try.to.split.this.String";
    String [] arrOfStr = str.split("\\.");
    for (String a : arrOfStr) {
        System.out.println(a);
    }
}

If the String consists of only the split character, the output will be an empty array.

public static void main(String [] args) {
    String str = "::::";
    String [] arrOfStr = str.split(":");
    System.out.println(arrOfStr.length);
}

The output will be 0.

Similarly, if you split an array on everything, the output will be nothing.

public static void main(String [] args) {
    String str = "java";
    String [] arrOfStr = str.split(".");
    System.out.println(arrOfStr.length);
}

The output will be output 0.

If you split an array on nothing, the output will be everything.

public static void main(String [] args) {
    String str = "java";
    String [] arrOfStr = str.split("");
    for (String a : arrOfStr) {
        System.out.println(a);
    }
}

Primitive values (like ints, doubles, and chars) do not provide methods. For example, you can't call equals on an int:

int i = 5;
System.out.println(i.equals(5)); // compiler error

But for each primitive type, there is a corresponding class in the Java library, called a wrapper class. We already spoke a bit about the wrapper class for char, Character.

For int it is called Integer. Other wrapper classes include Boolean, Long, and Double. They are in the java.lang package, so you can use them without importing them.

Each wrapper class defines constants MIN_VALUE and MAX_VALUE. For example, Integer.MIN_VALUE is -2147483648, and Integer.MAX_VALUE is 2147483647. Because these constants are available in wrapper classes, you don't have to remember them, and you don't have to include them in your programs.

Wrapper classes provide methods for converting Strings to other types. For example, Integer.parseInt() converts a String to (you guessed it) an integer:

String str = "12345";
int num = Integer.parseInt(str);

In this context, parse means something like “read and translate”.

The other wrapper classes provide similar methods, like Double.parseDouble() and Boolean.parseBoolean(). They also provide .toString(), which returns a String representation of a value:

int num = 12345;
String str = Integer.toString(num);

The result is the String "12345".

So far we have only written short programs that have a single class and a single method (main).

Now, we will expand our programs to utilize more than one method. But first, what is a method anyway?

A method in Java is a block of code that, when called, performs specific actions mentioned in it.

For instance, if you have written instructions to draw a circle in the method, it will do that task. You can insert values or parameters into methods, and they will only be executed when called. They are also referred to as functions.

The primary uses of methods in Java are:

• It allows code reusability (define once and use multiple times)
• It breaks a complex program into smaller chunks of code
• It increases code readability

We have seen methods before through our use of class objects. Classes such as Math, Character, and Scanner all have methods that help us simplify the work we need to do as programmers.

In mathematics, you have probably seen functions like sin and log, and you have learned to evaluate expressions like sin(π/2) and log(1/x).First, you evaluate the expression in parentheses, which is called the argument of the function. Then you can evaluate the function itself, maybe by punching it into a calculator.

Remember, we can use, or invoke, Math methods like this:

double root = Math.sqrt(17.0);
double angle = 1.5;
double height = Math.sin(angle);

The first line sets root to the square root of 17. The third line finds the sine of 1.5 (the value of angle).

We can change the values passed as arguments to these methods and they will use the same approach to compute the result based on this new value. That reusability is one of the main benefits of methods.

Just as with mathematical functions, Java methods can be composed. That means you can use one expression as part of another. For example, you can use any expression as an argument to a method:

double x = Math.cos(angle + Math.PI / 2.0);

This statement divides Math.PI by two, adds the result to angle, and computes the cosine of the sum. You can also take the result of one method and pass it as an argument to another:

double y = Math.exp(Math.log(10.0));

In Java, the log method always uses base e. So this statement finds the log base e of 10, and then raises e to that power. The result gets assigned to y.

Some Math methods take more than one argument. For example, Math.pow() takes two arguments and raises the first to the power of the second. This line of code assigns the value 1024.0 to the variable z:

double z = Math.pow(2.0, 10.0);

When using Math methods, it is a common error to forget the Math. For example, if you try to invoke pow(2.0, 10.0), you get an error message like:

The message "cannot find symbol" is confusing, but the last line provides a useful hint. The compiler is looking for pow in the same class where it is used, which is Test. If you don't specify a class name, the compiler looks in the current class.

You have probably guessed by now that we can define more than one method in a class, meaning that we can define our own methods for functionality.

There are a total of six components included in a method declaration. The components provide various information about the method:

1. Access Specifier


• This is used to define the access type of the method. Every method we write in this course will be public, however, Java provides four different specifiers, which are:


• public: You can access it from any class
• private: You can access it within the class where it is defined
• protected: Accessible only in the same package or other subclasses in another package
• default: It is the default access specifier used by the Java compiler if we don't mention any other specifiers. It is accessible only from the package where it is declared


2. Return Type


• This defines the return type of the method. We can declare the return type as void if the method returns no value.


3. Method Name


• This is used to give a unique name to the method. It will be referred by this name when we invoke it.


4. Parameter List


• This is a list of arguments (data type and variable name) that will be used in the method. It can also be kept blank if we don't want to use any parameters in the method.


5. Method Signature


• The method signature is just a combination of the method name and parameter list.


6. Method Body


• This is the set of instructions enclosed within curly brackets that the method will perform.

Here's an example:

public class NewLine {
    public static void newLine() {
        System.out.println();
    }

    public static void main(String [] args) {
        System.out.println("First line.");
        newLine(); //this is a method call 
        System.out.println("Second line.");
    }
}

The name of the class is NewLine. By convention, class names begin with a capital letter. NewLine contains two methods, newLine and main. Remember that Java is case-sensitive, so NewLine and newLine are not the same.

Method names should begin with a lowercase letter and use "camel case", which is a cute name for jammingWordsTogetherLikeThis. You can use any name you want for methods, except main or any of the Java keywords.

newLine and main are public, which means they can be invoked from other classes. They are both static.

When you declare a variable or a method as static, it belongs to the class, rather than a specific instance. This means that only one instance of a static member exists, even if you create multiple objects of the class, or if you don't create any. It will be shared by all objects.

And they are both void, which means that they don't yield a result (unlike the Math methods, for example).

The parentheses after the method name contain a list of variables, called parameters, where the method stores its arguments. The main method has a single parameter, called args, which has type String[]. That means that whoever invokes main must provide an array of Strings (we'll get to arrays in a later chapter).

Since newLine has no parameters, it requires no arguments, as shown when it is invoked in main. And because newLine is in the same class as main, we don't have to specify the class name.

What is the output of this program?

If we wanted more space between the two lines, we could invoke the same method repeatedly:

public static void main(String [] args) {
    System.out.println("First line.");
    newLine(); //call 1
    newLine(); //call 2
    newLine(); //call 3
    System.out.println("Second line.");
}

Or we could write a new method that displays three blank lines:

public static void threeLine() {
    newLine();
    newLine();
    newLine();
}
public static void main(String [] args) {
    System.out.println("First line.");
    threeLine();
    System.out.println("Second line.");
}

You can invoke the same method more than once, and you can have one method invoke another. In this example, main invokes threeLine, and threeLine invokes newLine().

Beginners often wonder why it is worth the trouble to create new methods. There are many reasons, but this example demonstrates a few of them:

• Creating a new method gives you an opportunity to give a name to a group of statements, which makes code easier to read and understand.
• Introducing new methods can make a program smaller by eliminating repetitive code. For example, to display nine consecutive new lines, you could invoke threeLine three times.
• A common problem solving technique is to break tasks down into subproblems. Methods allow us to focus on each sub-problem in isolation, and then compose them into a complete solution.

Pulling together the code from the previous section, the complete program looks like this:

public class NewLine {
    public static void newLine() {
        System.out.println();//4, 6, 8
    }

    public static void threeLine() {
        newLine();//3
        newLine();//5
        newLine();//7
    }

    public static void main(String[] args) {
        System.out.println("First line."); //1
        threeLine(); //2
        System.out.println("Second line."); //9
    }
}

When you look at a class definition that contains several methods, it is tempting to read it from top to bottom. But that is likely to be confusing, because that is not the flow of execution of the program.

Execution always begins at the first statement of main, regardless of where it is in the source file. Statements are executed one at a time, in order, until you reach a method invocation, which you can think of as a detour. Instead of going to the next statement, you jump to the first line of the invoked method, execute all the statements there, and then come back and pick up exactly where you left off.

That sounds simple enough, but remember that one method can invoke another one. In the middle of main, we go off to execute the statements in threeLine. While we are executing threeLine, we go off to execute newLine. Then newLine invokes println, which causes yet another detour.

Fortunately, Java is good at keeping track of which methods are running. So when println() completes, it picks up where it left off in newLine; when newLine completes, it goes back to threeLine, and when threeLine completes, it gets back to main.

In summary, when you read a program, don't read from top to bottom. Instead, follow the flow of execution.

Some of the methods we have used require arguments, which are the values you provide when you invoke the method. For example, to find the square root of a number, you have to provide the number, so Math.sqrt() takes a double as an argument.

To display a message, you have to provide the message, so println takes a String.

When you use a method, you provide the arguments. When you write a method, you name the parameters. The parameter list indicates what arguments are required.

The following shows an example:

public static void printTwice(String s) {
    System.out.println(s);
    System.out.println(s);
}
public static void main(String [] args) {
    printTwice("Don't make me say this twice!");
}

printTwice has a parameter named s with type String. When we invoke printTwice, we have to provide an argument with type String.

Before the method executes, the argument gets assigned to the parameter. In this example, the argument "Don't make me say this twice!" gets assigned to the parameter s.

This process is called parameter passing because the value gets passed from outside the method to the inside. An argument can be any kind of expression, so if you have a String variable, you can use it as an argument:

String argument = "Never say never.";
printTwice(argument);

The value you provide as an argument must have the same type as the parameter. For example, if you try:

printTwice(17); // syntax error

You will get an error message.

Sometimes Java can convert an argument from one type to another automatically.

For example, Math.sqrt() requires a double, but if you invoke Math.sqrt(25), the integer value 25 is automatically converted to the floating point value 25.0. But in the case of printTwice, Java can't (or won't) convert the integer 17 to a String.

Parameters and other variables only exist inside their own methods. Inside main, there is no such thing as s. If you try to use it there, you'll get a compiler error. Similarly, inside printTwice there is no such thing as argument. That variable belongs to main.

Because variables only exist inside the methods where they are defined, they are often called local variables.

Here is an example of a method that takes two parameters:

public static void printTime(int hour, int minute) {
    System.out.print(hour);
    System.out.print(":");
    System.out.println(minute);
}

In the parameter list, it may be tempting to write:

public static void printTime(int hour, minute) {

But that format (without the second int) is only legal for variable declarations. In parameter lists, you need to specify the type of each variable separately.

To invoke this method, we have to provide two integers as arguments:

int hour = 11;
int minute = 59;
printTime(hour, minute);

A common error is to declare the types of the arguments, like this:

int hour = 11;
int minute = 59;
printTime(int hour, int minute); // syntax error

That's a syntax error; the compiler sees int hour and int minute as variable declarations, not expressions. You wouldn't declare the types of the arguments if they were simply integers:

printTime(int 11, int 59); // syntax error

Pulling together the code fragments from the previous section, here is a complete class definition:

public class PrintTime {
    public static void printTime(int hour, int minute) {
        System.out.print(hour);
        System.out.print(":");
        System.out.println(minute);
    }
    public static void main(String[] args) {
        int hour = 11;
        int minute = 59;
        printTime(hour, minute);
    }
}

printTime has two parameters, named hour and minute. And main has two variables, also named hour and minute.

Although they have the same names, these variables are not the same. hour in printTime and hour in main refer to different storage locations, and they can have different values.

For example, you could invoke printTime like this:

int hour = 11;
int minute = 59;
printTime(hour + 1, 0);

Before the method is invoked, Java evaluates the arguments; in this example, the results are 12 and 0. Then it assigns those values to the parameters. Inside printTime, the value of hour is 12, not 11, and the value of minute is 0, not 59.

Furthermore, if printTime modifies one of its parameters, that change has no effect on the variables in main.

One way to keep track of everything is to draw a stack diagram, which is a state diagram that shows method invocations.

For each method there is a box called a frame that contains the method's parameters and variables. The name of the method appears outside the frame; the variables and parameters appear inside.

As with state diagrams, stack diagrams show variables and methods at a particular point in time. The following is a stack diagram at the beginning of the printTime method.

A nice feature of the Java language is the ability to embed documentation in your source code. That way, you can write it as you go, and as things change, it is easier to keep the documentation consistent with the code.

If you include documentation in your source code, you can extract it automatically, and generate well-formatted HTML, using a tool called Javadoc

This tool is included in standard Java development environments, and it is widely used. In fact, the online documentation of the Java libraries is generated by Javadoc.

Javadoc scans your source files looking for specially-formatted documentation comments, also known as “Javadoc comments”. They begin with /** (two stars) and end with */ (one star). Anything in between is considered part of the documentation.

Here's a class definition with two Javadoc comments, one for the class and one for the main method:

/**
 * Example program that demonstrates print vs println.
 */
public class Goodbye {
    /**
     * Prints a greeting.
     */
    public static void main(String [] args) {
        System.out.print("Goodbye, "); // note the space
        System.out.println("cruel world");
    } 
}

The class comment explains the purpose of the class. The method comment explains what the method does.

Notice that this example also includes an inline comment, beginning with //. In general, inline comments are short phrases that help explain complex parts of a program. They are intended for other programmers reading and maintaining the source code.

In contrast, Javadoc comments are longer, usually complete sentences. They explain what each method does, but they omit details about how the method works. And they are intended for people who will use the methods without looking at the source code.

Appropriate comments and documentation are essential for making source code readable. And remember that the person most likely to read your code in the future, and appreciate good documentation, is you.

Some of the methods we have used, like the Math methods, return values. But all the methods we have written so far have been void; that is, they don't return values. Now, we will begin discuss how to write methods that return values, which we call value methods.

When you invoke a void method, the invocation is usually on a line all by itself.

For example, here is a recursive method called countDown():

public static void countDown(int n) {
    if (n == 0) {
        System.out.println("Blastoff!");
    } else {
        System.out.println(n);
        countDown(n - 1);
    }
}

And here is how it is invoked:

countDown(3);

On the other hand, when you invoke a value method, you have to do something with the return value. We usually assign it to a variable or use it as part of an expression, like this:

double error = Math.abs(expected - actual);
double height = radius * Math.sin(angle);

Compared to void methods, value methods differ in two ways:

• They declare the type of the return value (the return type);
• They use at least one return statement to provide a return value.

Here's an example: calculateArea() takes a double as a parameter and returns the area of a circle with that radius:

public static double calculateArea(double radius) {
    double result = Math.PI * radius * radius;
    return result;
}

As usual, this method is public and static. But in the place where we are used to seeing void, we see double, which means that the return value from this method is a double.

The last line is a new form of the return statement that includes a return value. This statement means, "return immediately from this method and use the following expression as the return value."

The expression you provide can be arbitrarily complex, so we could have written this method more concisely:

public static double calculateArea(double radius) {
    return Math.PI * radius * radius;
}

On the other hand, temporary variables like result often make debugging easier, especially when you are stepping through code using an interactive debugger.

The type of the expression in the return statement must match the return type of the method. When you declare that the return type is double, you are making a promise that this method will eventually produce a double value.

If you try to return with no expression, or an expression with the wrong type, the compiler will generate an error.

Sometimes it is useful to have multiple return statements, for example, one in each branch of a conditional:

public static double absoluteValue(double x) {
    if (x < 0) {
        return -x;
    } else {
        return x;
    }
}

Since these return statements are in a conditional statement, only one will be executed. As soon as either of them executes, the method terminates without executing any more statements.

Code that appears after a return statement (in the same block), or any place else where it can never be executed, is called dead code. The compiler will give you an "unreachable statement" error if part of your code is dead.

For example, this method contains dead code:

public static double absoluteValue(double x) {
    if (x < 0) {
        return -x;
    } else {
        return x;
    }
    System.out.println("This line is dead.");
}

If you put return statements inside a conditional statement, you have to make sure that every possible path through the program reaches a return statement. The compiler will let you know if that's not the case.

For example, the following method is incomplete:

public static double absoluteValue(double x) {
    if (x < 0) {
        return -x;
    } else if (x > 0) {
        return x;
    }
    // syntax error
}

When x is 0, neither condition is true, so the method ends without hitting a return statement. The error message in this case might be something like "missing return statement", which is confusing since there are already two of them. But hopefully you will know what it means.

Beginners often make the mistake of writing a lot of code before they try to compile and run it. Then they spend way too much time debugging. A better approach is what we call incremental development.

The key aspects of incremental development are:

• Start with a working program and make small, incremental changes. At any point, if there is an error, you will know where to look.
• Use variables to hold intermediate values so you can check them, either with print statements or by using a debugger.
• Once the program is working, you can consolidate multiple statements into compound expressions (but only if it does not make the program more difficult to read).

As an example, suppose you want to find the distance between two points, given by the coordinates (x1, y1) and (x2, y2). By the usual definition:

The first step is to consider what a distance method should look like in Java. In other words, what are the inputs (parameters) and what is the output (return value)? In this case, the two points are the parameters, and it is natural to represent them using four double values. The return value is the distance, which should also have type double.

Already we can write an outline for the method, which is sometimes called a stub. The stub includes the method signature and a return statement:

public static double distance(double x1, double y1, double x2, double y2) {
    return 0.0;
}

The return statement is a placeholder that is necessary for the program to compile. At this stage the program doesn't do anything useful, but it is good to compile it so we can find any syntax errors before we add more code.

It's usually a good idea to think about testing before you develop new methods; doing so can help you figure out how to implement them. To test the method, we can invoke it from main using sample values:

double dist = distance(1.0, 2.0, 4.0, 6.0);

With these values, the horizontal distance is 3.0 and the vertical distance is 4.0. So the result should be 5.0, the hypotenuse of a 3-4-5 triangle. When you are testing a method, it is helpful to know the right answer.

Once we have compiled the stub, we can start adding lines of code one at a time. After each incremental change, we recompile and run the program. If there is an error at any point, we have a good idea where to look: the last line we added.

The next step is to find the differences x2 − x1 and y2 − y1. We store those values in temporary variables named dx and dy.

public static double distance(double x1, double y1, double x2, double y2) {
    double dx = x2 - x1;
    double dy = y2 - y1;
    System.out.println("dx is " + dx);
    System.out.println("dy is " + dy);
    return 0.0;
}

The print statements allows us to check the intermediate values before proceeding. They should be 3.0 and 4.0. We will remove the print statements when the method is finished. Code like that is called scaffolding, because it is helpful for building the program, but it is not part of the final product.

The next step is to square dx and dy. We could use the Math.pow method, but it is simpler to multiply each term by itself.

public static double distance(double x1, double y1, double x2, double y2) {
    double dx = x2 - x1;
    double dy = y2 - y1;
    double dsquared = dx * dx + dy * dy;
    System.out.println("dsquared is " + dsquared);
    return 0.0;
}

Again, you should compile and run the program at this stage and check the intermediate value, which should be 25.0. Finally, we can use Math.sqrt to compute and return the result.

public static double distance(double x1, double y1, double x2, double y2) {
    double dx = x2 - x1;
    double dy = y2 - y1;
    double dsquared = dx * dx + dy * dy;
    double result = Math.sqrt(dsquared);
    return result;
}

As you gain more experience programming, you might write and debug more than one line at a time. Nevertheless, incremental development can save you a lot of time.

Once you define a new method, you can use it as part of an expression, or build new methods using existing methods.

For example, suppose someone gave you two points, the center of the circle and a point on the perimeter, and asked for the area of the circle. Let's say the center point is stored in the variables xc and yc, and the perimeter point is in xp and yp.

The first step is to find the radius of the circle, which is the distance between the two points. Fortunately, we have just written a method that does just that (distance).

double radius = distance(xc, yc, xp, yp);

The second step is to find the area of a circle with that radius. We have a written a method for that computation too (calculateArea).

double area = calculateArea(radius);
return area;

Putting everything together in a new method, we get:

public static double circleArea(double xc, double yc, double xp, double yp) {
    double radius = distance(xc, yc, xp, yp);
    double area = calculateArea(radius);
    return area;
}

The temporary variables radius and area are useful for development and debugging, but once the program is working we can make it more concise by composing the method calls:

public static double circleArea(double xc, double yc, double xp, double yp) {
    return calculateArea(distance(xc, yc, xp, yp));
}

This example demonstrates a process called functional decomposition; that is, breaking a complex computation into simple methods, testing the methods in isolation, and then composing the methods to perform the computation. This process reduces debugging time and yields code that is more likely to be correct and easier to maintain.

You might have noticed that circleArea and calculateArea perform similar functions. They both find the area of a circle, but they take different parameters. For calculateArea, we have to provide the radius; for circleArea we provide two points.

If two methods do the same thing, it is natural to give them the same name. Having more than one method with the same name is called overloading, and it is legal in Java as long as each version takes different parameters. So we could rename circleArea to calculateArea:

public static double calculateArea(double xc, double yc, double xp, double yp) {
    return calculateArea(distance(xc, yc, xp, yp));
}

Note that this new calculateArea method is not recursive. When you invoke an overloaded method, Java knows which version you want by looking at the arguments that you provide. If you write:

double x = calculateArea(3.0);

Java looks for a method named calculateArea that takes one double as an argument, and so it uses the first version, which interprets the argument as a radius. If you write:

double y = calculateArea(1.0, 2.0, 4.0, 6.0);

Java uses the second version of calculateArea, which interprets the arguments as two points. In this example, the second version actually invokes the first version.

Many Java methods are overloaded, meaning that there are different versions that accept different numbers or types of parameters. For example, there are versions of print and println that accept a single parameter of any data type. In the Math class, there is a version of abs that works on doubles, and there is also a version for ints.

Although overloading is a useful feature, it should be used with caution. You might get yourself nicely confused if you are trying to debug one version of a method while accidentally invoking a different one.

Methods can return boolean values, just like any other type, which is often convenient for hiding tests inside methods.

For example:

public static boolean isSingleDigit(int x) {
    if (x > -10 && x < 10) {
        return true;
    } else {
        return false;
    }
}

The name of this method is isSingleDigit(). It is common to give boolean methods names that sound like yes/no questions. Since the return type is boolean , the return statement has to provide a boolean expression.

The code itself is straightforward, although it is longer than it needs to be. Remember that the expression x > -10 && x < 10 has type boolean, so there is nothing wrong with returning it directly (without the if statement):

public static boolean isSingleDigit(int x) {
    return x > -10 && x < 10;
}

In main, you can invoke the method in the usual ways:

System.out.println(isSingleDigit(2));
boolean bigFlag = !isSingleDigit(17);

The first line displays true because 2 is a single-digit number. The second line sets bigFlag to true, because 17 is not a single-digit number.

Conditional statements often invoke boolean methods and use the result as the condition:

if (isSingleDigit(z)) {
    System.out.println("z is small");
} else {
    System.out.println("z is big");
}

Examples like this one almost read like English: "If is single digit z, print ... else print ...".

We discussed how to write documentation comments using /**. It's generally a good idea to document each class and method, so that other programmers can understand what they do without having to read the code.

To organize the documentation into sections, Javadoc supports optional tags that begin with the at sign (@). For example, we can use @param and @return to provide additional information about parameters and return values.

/**
  * Tests whether x is a single digit integer.
  *
  * @param x the integer to test
  * @return true if x has one digit, false otherwise
  */
public static boolean isSingleDigit(int x) {

The following shows part of the resulting HTML page generated by Javadoc. Notice the relationship between the source code and the documentation:

Methods with multiple parameters should have separate @param tags that describe each one. Void methods should have no @return tag, since they do not return a value.

An array is a sequence of values; the values in the array are called elements.

Conceptually this might sound familiar, internally Strings are represented by a char array with an offset and length (this allows to create lightweight substrings, using the same char arrays).

However, Strings are actually immutable objects representing a character sequence (CharSequence is one of the interfaces implemented by String). The main difference to char arrays and collections of chars is that Strings cannot be modified, so it's not possible (ignoring reflection) to add/remove/replace characters.

You can make an array of ints, doubles, or any other type, but all the values in an array must have the same type.

To create an array, we have to declare a variable with an array type and then create the array itself. Array types look like other Java types, except they are followed by square brackets ([]).

For example, the following lines declare that counts is an "integer array" and values is a "double array":

int [] counts;
double [] values;

To create the array itself, we have to use the new operator, which we have seen with Scanner and PrintWriter:

counts = new int [4];
values = new double [size];

The first assignment makes count refer to an array of four integers. The second makes values refer to an array of double, where the number of elements in values depends on the value of size.

Of course, we can also declare the variable and create the array in a single line of code:

int [] counts = new int [4];
double [] values = new double [size];

You can use any integer expression for the size of an array, as long as the value is nonnegative. If you try to create an array with -4 elements, for example, you will get a NegativeArraySizeException. An array with zero elements is allowed, and there are special uses for such arrays that we'll see later on.

Another way to create an array is to use an initializer list. You can initialize (set) the values in the array to a list of values in curly brackets { } when you create it, like below. In this case you don't specify the size of the array, it will be determined from the number of values that you specify.

For example:

int [] counts = {0, 0, 0, 0};

When you create an array of ints, the elements are initialized to zero. The following is a state diagram of the counts array so far:

The arrow indicates that the value of counts is a reference to the array. You should think of the array and the variable that refers to it as two different things. As we’ll soon see, we can assign a different variable to refer to the same array, and we can change the value of counts to refer to a different array.

The large numbers inside the boxes are the elements of the array. The small numbers outside the boxes are the indexes (or indices) used to identify each location in the array. Notice that the index of the first element is 0, not 1, as you might have expected. (We should remember this from Strings!)

The [] operator selects elements from an array:

System.out.println("The zeroth element is " + counts[0]);

You can use the [] operator anywhere in an expression:

counts[0] = 7;
counts[1] = counts[0] * 2;
counts[2]++;
counts[3] -= 60;

The following shows the result of these statements:

You can use any expression as an index, as long as it has type int.

One of the most common ways to index an array is with a loop variable.

For example:

int i = 0;
while (i < 4) {
    System.out.println(counts[i]);
    i++;
} 

This while loop counts from 0 up to 4. When i is 4, the condition fails and the loop terminates. So the body of the loop is only executed when i is 0, 1, 2, and 3.

Each time through the loop we use i as an index into the array, displaying the ith element. This type of array processing is often written using a for loop

for (int i = 0; i < 4; i++) {
    System.out.println(counts[i]);
}

For the counts array, the only legal indexes are 0, 1, 2, and 3. If the index is negative or greater than 3, the result is an ArrayIndexOutOfBoundsException.

You can use println to display an array, but it probably doesn’t do what you would like.

For example, the following fragment:

1. declares an array variable,
2. makes it refer to an array of four elements, and
3. attempts to display the contents of the array using println:

int [] a = {1, 2, 3, 4};
System.out.println(a);

Unfortunately, the output is something like: [I@bf3f7e0

The bracket indicates that the value is an array, I stands for “integer”, and the rest represents the address of the array.

If we want to display the elements of the array, we can do it ourselves:

public static void printArray(int [] a) {
    System.out.print("{" + a[0]);
    for (int i = 1; i < a.length; i++) {
        System.out.print(", " + a[i]);
    }
    System.out.println("}");
}

Given the previous array, the output of this method is: {1, 2, 3, 4}

The Java library provides a utility class java.util.Arrays that provides methods for working with arrays. One of them, toString(), returns a String representation of an array. We can invoke it like this:

System.out.println(Arrays.toString(a));

And the output is: [1, 2, 3, 4]

As usual, we have to import java.util.Arrays before we can use it. Notice that the String format is slightly different: it uses square brackets instead of curly braces. However, sometimes it is beneficial for us to write our own printArray() method, if we want our output formatted in a particular way.

As previously explained, array variables contain references to arrays. When you make an assignment to an array variable, it simply copies the reference. But it doesn't copy the array itself!

For example:

double [] a = new double [3];
double [] b = a;

These statements create an array of three doubles and make two different variables refer to it, as shown below:

Any changes made through either variable will be seen by the other. For example, if we set a[0] = 17.0, and then display b[0], the result is 17.0. Because a and b are different names for the same thing, they are sometimes called aliases.

If you actually want to copy the array, not just a reference, you have to create a new array and copy the elements from the old to the new, like this:

double [] b = new double [3];
for (int i = 0; i < 3; i++) {
    b[i] = a[i];
}

The examples in the previous section only work if the array has three elements. It would be better to generalize the code to work with arrays of any size. We can do that by replacing the magic number, 3, with a.length:

double [] b = new double [a.length];
for (int i = 0; i < a.length; i++) {
    b[i] = a[i];
}

All arrays have a built-in constant, length, that stores the number of elements. The expression a.length may look like a method invocation, but there are no parentheses and no arguments.

The last time this loop gets executed, i is a.length - 1, which is the index of the last element. When i is equal to a.length, the condition fails and the body is not executed - which is a good thing, because trying to access a[a.length] would throw an exception.

Many computations can be implemented by looping through the elements of an array and performing an operation on each element.

For example, the following loop squares the elements of a double array:

for (int i = 0; i < a.length; i++) {
    a[i] = Math.pow(a[i], 2.0);
}

Looping through the elements of an array is called a traversal.

Another common pattern is a search, which involves traversing an array looking for a particular element.

For example, the following method takes an int array and an integer value, and it returns the index where the value appears:

public static int search(double [] a, double target) {
    for (int i = 0; i < a.length; i++) {
        if (a[i] == target) {
            return i;
        }
    }
    return -1;
}

If we find the target value in the array, we return its index immediately. If the loop exits without finding the target, it returns -1, a special value chosen to indicate a failed search.

Another common traversal is a reduce operation, which "reduces" an array of values down to a single value. Examples include the sum or product of the elements, the minimum, and the maximum.

The following method takes a double array and returns the sum of the elements:

public static double sum (double [] a) {
    double total = 0.0;
    for (int i = 0; i < a.length; i++) {
        total += a[i];
    }
    return total;
}

Before the loop, we initialize total to zero. Each time through the loop, we update total by adding one element from the array. At the end of the loop, total contains the sum of the elements. A variable used this way is sometimes called an accumulator.

We spoke prior about using the Math class method, Math.random() to generate random numbers. How can this be relevant for arrays?

As previously mentioned, most computer programs do the same thing every time they run; programs like that are deterministic. Usually determinism is a good thing, since we expect the same calculation to yield the same result. But for some applications, we want the computer to be unpredictable. Games are an obvious example, but there are many others.

Making a program nondeterministic turns out to be hard, because it is hard for a computer to generate truly random numbers. But there are algorithms that generate unpredictable sequences called pseudorandom numbers. For most applications, they are as good as random.

The following code creates an int array and fills it with random numbers between 0 and 99, then displays it using the printArray() we just discussed:

public static void main (String [] args) {
    final int SIZE = 10;
    int max = 100;
    int min = 1;
    int [] a = new int [SIZE];
    for (int i = 0; i < a.length; i++) {
        int rand = (int) (Math.random() * (max - min) + min);
        a[i] = rand;
    }
    printArray(a);
}

The output looks something like this:

{99, 47, 18, 51, 86, 55, 21, 88, 50, 67}

If you run it, you will probably get different values.

If these values were exam scores -- and they would be pretty bad exam scores -- the teacher might present them to the class in the form of a histogram. In statistics, a histogram is a set of counters that keeps track of the number of times each value appears.

For exam scores, we might have ten counters to keep track of how many students scored in the 90s, the 80s, etc. To do that, we can traverse the array and count the number of elements that fall in a given range.

The following method takes an array and two integers, low and high. It returns the number of elements that fall in the range from low to high.

public static int inRange (int [] a, int low, int high) {
    int count = 0;
    for (int i = 0; i < a.length; i++) {
        if (a[i] >= low && a[i] < high) {
            count++;
        }
    }
    return count;
}

This pattern should look familiar: it is another reduce operation. Notice that low is included in the range (>=), but high is excluded (<). This detail keeps us from counting any scores twice.

Now we can count the number of scores in each grade range:

public static void main (String [] args) {
    final int SIZE = 10;
    int max = 100;
    int min = 1;
    int [] scores = new int [SIZE];
    for (int i = 0; i < scores.length; i++) {
        int rand = (int) (Math.random() * (max - min) + min);
        scores[i] = rand;
    }
    printArray(scores);

    int a = inRange(scores, 90, 100);
    int b = inRange(scores, 80, 90);
    int c = inRange(scores, 70, 80);
    int d = inRange(scores, 60, 70);
    int f = inRange(scores, 0, 60);
}

The previous code is repetitious, but it is acceptable as long as the number of ranges is small. But suppose we wanted to keep track of the number of times each score appears. We would have to write 100 lines of code:

int count0 = inRange(scores, 0, 1);
int count1 = inRange(scores, 1, 2);
int count2 = inRange(scores, 2, 3);
...
int count99 = inRange(scores, 99, 100);

What we need is a way to store 100 counters, preferably so we can use an index to access them. In other words, we need another array!

The following fragment creates an array of 100 counters, one for each possible score. It loops through the scores and uses inRange to count how many times each score appears. Then it stores the results in the array:

int [] counts = new int [100];
for (int i = 0; i < counts.length; i++) {
    counts[i] = inRange(scores, i, i + 1);
}

Notice that we are using the loop variable i three times: as an index into the counts array, and as two arguments for inRange(). The code works, but it is not as efficient as it could be. Every time the loop invokes inRange(), it traverses the entire array.

It would be better to make a single pass through the array, and for each score, compute which range it falls in and increment the corresponding counter. This code traverses the array of scores only once to generate the histogram:

int [] counts = new int [100];
for (int i = 0; i < scores.length; i++) {
    int index = scores[i];
    counts[index]++;
}

Each time through the loop, it selects one element from scores and uses it as an index to increment the corresponding element of counts. Because this code only traverses the array of scores once, it is much more efficient.

Since traversing arrays is so common, Java provides an alternative syntax that makes the code more compact.

For example, consider a for loop that displays the elements of an array on separate lines:

for (int i = 0; i < values.length; i++) {
    int value = values[i];
    System.out.println(value);
}

We could rewrite the loop like this:

for (int value : values) {
    System.out.println(value);
}

This statement is called an enhanced for loop or a for-each loop. You can read it as, "for each value in values". It is conventional to use plural nouns for array variables and singular nouns for element variables.

Notice how the single line for (int value : values)replaces the first two lines of the standard for loop. It hides the details of iterating each index of the array, and instead, focuses on the values themselves.

Using the enhanced for loop, and removing the temporary variable, we can write the histogram code from the previous section more concisely:

int [] counts = new int[100];
for (int score : scores) {
    counts[score]++;
}

Enhanced for loops often make the code more readable, especially for accumulating values. But they are not helpful when you need to refer to the index, as in search operations.

for (double d : array) {
    if (d == target) {
        // array contains d, but we don't know the index
    }
}

Passing arrays to methods is similar to passing primitive data types. However, there is one key difference that needs to be kept in mind. Primitive data types are considered "pass-by-value" while arrays mimic a concept called "pass-by-reference", meaning that when an array is passed as an argument, its memory address location (its "reference") is used.

When passing a primitive data type as a parameter, you are passing a copy of the data. Therefore, changes made to the data are lost when the method returns unless the data is returned, i.e. the caller and callee have two independent variables with the same value. If the callee modifies the parameter value, the effect is not visible to the caller.

When passing an array as a parameter you are passing a pointer to the arrays memory location. Therefore, changes made to the array in the method are kept even when the method returns. In this way, the contents of an array CAN be changed inside of a method, since we are dealing directly with the actual array and not with a copy of the array.

⚠️You will need to be careful when sending an array to a method. Remember that any changes made to the array in the method will change the data in the original array. Be sure that your intention is to change the original data (thus losing the original data).⚠️

To pass an array of variables it is identical to passing a single variable with the exception of placing a "[]" between your Variable type and your variable name like so:

public static int add(int [] x){}

The following is a method named add that passes an array as a parameter, calculates the sum of the array elements and returns the sum:

public static int add(int [] x){
    int sum = 0;
    for(int i = 0; i < x.length; i++)
        sum = sum + x[i];
              
    return sum;
} 

Calling the method is exactly the same as if you were sending a single value variable:

int [] x = {1, 2};
int sum = add(x);

Another example:

public static void main(String [] args) {
    int [] num = {1, 2, 3};
    for(int i = 0; i < num.length; i++){
        System.out.println("num[" + i + "] = " + num[i]);
    }
    
    System.out.println("Now, call the method.");

    testArray(num);// Method call
    for(int j = 0; j < num.length; j++){
      System.out.println("num[" + j + "] = " + num[j]);
  }
}

public static void testArray(int [] value){
    value[0] = 4;
    value[1] = 5;
    value[2] = 6;
}

What do we expect this code to print?

When working with arrays, we will come across situations where some array indexes contain a value, while others do not. These arrays are said to be 'partially filled'.

A partially filled array is an array that has indexes that aren't being used to store data. The size of an array is set when it is initialized and cannot be changed afterwards. So, we initialize an array with a size large enough to hold the maximum amount of data that needs to be stored.

The following image displays what a typical partially filled array looks like. Notice that indexes 4,5,6 and 7 have not been populated by any data. The lack of data in these indexes is what makes this a partially filled array.

Partially filled arrays are normally instantiated using a constant variable that defines the maximum array size (capacity). A size variable is created to keep track of the current size of your partially filled array. The size variable also allows you to ensure that you are not exceeding the maximum size.

For example:

public static void main(String [] args){
    final int CAPACITY = 100; //determines total size of array
    int [] partialArray = new int[CAPACITY]; 
    int size = 0; //keeps track of the size of partialArray
}

Handling partially filled arrays is very similar to handling full arrays. The difference is that you must include a size variable and update it when you add and remove data from the array.

The obvious value to choose when determining if an index is empty is the default value that a variable is assigned when the variable is created. Recall that when you create a String variable, its default value is null. Meanwhile, for ints, doubles, and chars, their default values are 0. Lastly, the default value for a boolean variable is false.

While using the default value may work well in some cases (using the default works well for Strings), the default value will not work for all cases. In particular, using the default value to define the empty index in an array of ints or doubles can usually lead to problems.

For example, suppose you have a program which stores an assignment mark out of 10 for a group of students in an array of type int. Each index in the array corresponds to one students mark. If you use the default value to define an empty index, it will be impossible to tell the difference between students whose assignments have not been marked, and students who got a mark of 0.

In order to avoid cases where the default value conflicts with possible array values, you need to initialize the array to something different.

In the above scenario, the problem of 0 being both an empty index and an input value can be solved by initializing the array index values to -1. The code snippet below shows some example code as to what the initialization code might look like:

 public static void main(String [] args){
    final int TOTAL_STUDENTS = 30;
    int [] gradeArray = new int[TOTAL_STUDENTS];
            
    for(int i = 0; i < gradeArray.length; i++) { //go through all indexes
        gradeArray[i] = -1; //set each index to -1
    }
} 

While initializing the array index values to -1 works well in the assignment mark example, it obviously wouldn't work if -1 was a valid input value. However, in the above example, we are following a more general rule: always define your empty index such that it can not be mistaken for a valid input value.

Most programs will have a separate method for adding and deleting data from a partially filled array. You will need to pass the size variable anytime you need to access the contents of partialArray. When working with a partially filled array where array values are added and removed, your array may fill up to maximum capacity. By comparing the size and CAPACITY variables, you can quickly determine if new values can be added to the array.

For example, we can insert data by first checking whether or not we have met the capacity of the array:

public static void insert(int [] partialArray, int size){
    if (size < partialArray.length) { //check to ensure size is less than capacity
        partialArray[size] = 50; //or whatever value needs to be added here
        size++; //increase the # of values in array
    }
}

The same logic can be applied to removing something from the END of the data list:

public static void delete(int [] partialArray, int size){
    if (size > 0){
        partialArray[size-1] = 0;  // size-1 is the last index containing data
        size--;
    }
}

We just talked about removing an element from the end of our data list, but what if we needed to remove an element from the middle of the array?

What does it mean to remove an element from an array? The problem with Java arrays (and arrays in many languages) is the array is fixed in length. This means you can't easily remove elements from an array.

However we can shift elements, which for our purposes is almost the same.

To remove an array element at index i, you shift elements with index greater than i left (or down) by one element. For example, if you want to remove element 3, you copy element 4 to element 3, element 5 to element 4, element 6 to element 5, ... etc.

In other words, you copy element j + 1 to element j, where j ranges from i (which is the element we want to remove) up to the length of the array minus 2. (Minus 2? Why 2? We'll see soon).

This way we preserve the "order" of the array.

For example, think of the array as a line of students waiting to get tickets to an event. Suppose one student leaves the line. We can think of the student being "removed" from the line. When this student is removed, all of the students behind should move up one step. For example, if the student standing 3rd in line leaves, then the student that's 4th in line becomes 3rd. The one that's 5th in line becomes 4th, and so forth.

Let's say we have a roster of students waitlisted for a particular class and we want to remove a specific student from the middle of the roster (let's say they are no longer interested). We can achieve this by first finding the index of the student we want to remove and then using that index to remove the student from the roster.

String [] roster = {"Alice", "Bob", "Charlie", "David", "Eve"};

We can treat index 0 as the front of the line and the index, length - 1, as the end of the line. Once we identify the student who has left the waitlist, let's say Charlie, we can find their location using a searching algorithm (in this case, Charlie is located at index 2)

We can now start shifting up from that index (not from the beginning as indexes 0 and 1 are not affected by this modification):

public static void removeElt(int [] arr, int remIndex){
    for(int i = remIndex; i < arr.length - 1; i++){
        arr[i] = arr[i + 1] ; 
    }
}

Notice that we used arr.length - 1 instead of arr.length. Why?

What's the maximum value that i reaches, but where the condition still evaluates to true?

Answer: the maximum value of i where we still enter the loop body is arr.length - 2.

Let's plug in arr.length - 2 for i and see what happens. This is basically what happens on the last iteration of the loop:

arr[arr.length - 2] = arr[(arr.length - 2) + 1];

which is just:

arr[arr.length - 2] = arr[arr.length - 1];

This is a valid assignment. We are copying the last element of the array (i.e., element arr.length - 1) to the next to last element (i.e., element arr.length - 2).

You'll notice that the students each get shifted to the left by 1 starting from "David" replacing "Charlie". However, the last element is still "Eve" (there are now two "Eve"s!).

This kind of removing leaves the last element (i.e., the element at the maximum index) unchanged.

Is that OK? Usually, it's fine. You might be tempted to set it to 0 (if numerical) or null (in our case, Strings) or some other value, but if there's no compelling reason to do so, you can leave it alone.

However, for this case, to avoid duplicate students we should set the last element to null and keep track of how many students are actually on the list (making it a partially filled array).

Sometimes we need multiple types of data that all apply to the same particular record. Think of a spreadsheet containing student names and test scores.

Despite being separate data (student names and numerical test scores respectively), a pair of them can both be attributed to the same person (they are not independent of one another)

int [] highScores = {99,98,98,88,68};
String [] names = {"Jamal", "Emily", "Destiny", "Mateo", "Sofia"};

The data type of the arrays themselves do not need to match (as one is String and one is int) However, to be parallel they do need to be both of the same size (every student has a corresponding grade)

Parallel arrays are several arrays with the same number of elements that work in tandem to organize data.

Parallel arrays come in handy when data regarding different characteristics of the same subject of interest needs to be stored and accessed efficiently.

Let's look at the following arrays representing the data from a dog show:

String [] dogName = {"Wally", "Skeeter", "Corky", "Jessie", "Sadie"};
int [] round1 = {18,22,12,17,15};
int [] round2 = {20,25,16,18,17};

In the data represented above, the first array is the dog's name, the second array is the dog's score in round 1 of the competition, and the third array is the dog's score in round 2 of the competition. The dog in the first element of the first array has the scores represented in the first elements of the second and third arrays. Notice that the arrays do not all contain the same "type" of data Such data, can be stored using parallel arrays.

Now we can print out the arrays:

//Printing the dog competition information:
for(int index = 0; index < dogName.length; index++){
    System.out.print("Contestant #" + (index+1) + ": " + dogName[index] + " ");
    System.out.print("Round 1: " + round1[index] + " ");
    System.out.print("Round 2: " + round2[index] + " ");
    System.out.println("Total score: " + (round1[index]+round2[index]));
}

Another example: The program below implements four parallel arrays. The first, second, third, and fourth arrays store the names, ages, grades, and the subjects of five students, respectively.

Due to the semantics of parallel arrays, each array is of the same size, and each array element at the same index in all four arrays corresponds to the same student, who will be our subject of interest.

Using one for loop, all characteristics of each student are accessed and printed:

String [] fname = {"John", "Michael", "Sara", "Zubair", "Sadia"};
int [] age = {18,19,18,19,19};
char [] grade = {'B','A','B','A','A'};
String [] subject =  {"English", "Math", "History", "Physics", "Chemistry"};
for (int i = 0; i < fname.length; i++) {
  System.out.print("My name is " + fname[i] + ". I am " + age[i]);
  System.out.print(" years old. I have a grade of " + grade[i]); 
  System.out.println(" in my favorite subject: " + subject[i] + "!");
}

We spoke a bit about searching arrays so far, and we have always done it like this:

public static int search(String [] roster, String student) {
    for (int i = 0; i < roster.length; i++) {
        if (roster[i].equals(student)) {
            return i;
        }
    }
    return -1;
}

This version of search uses the algorithm we are most familiar with, which is called linear (sequential) search

Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set.

In the Linear Search Algorithm:

• Every element is considered as a potential match for the key and checked for the same
• If any element is found equal to the key, the search is successful and the index of that element is returned
• If no element is found equal to the key, the search yields “No match found”

We can define the algorithm with four main steps:

For example: Consider the array int [] arr = {10, 50, 30, 70, 80, 20, 90, 40} and key (the element we are searching for) = 30

We will start searching from the first element (index 0) and compare the key with each element (arr[i])

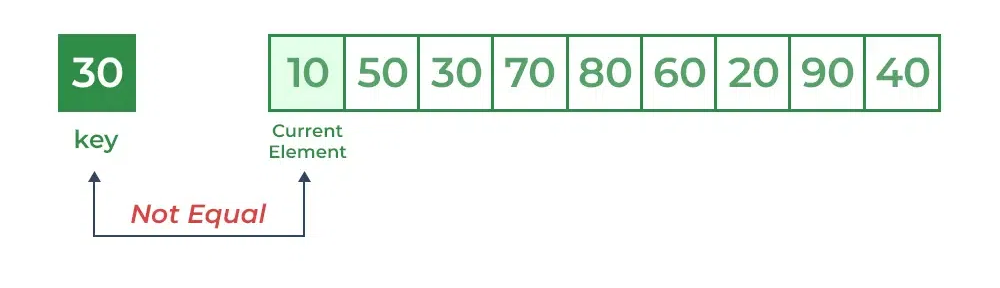
Comparing the key with first element arr[0]. Since they are not equal, the iterator moves to the next element as a potential match.

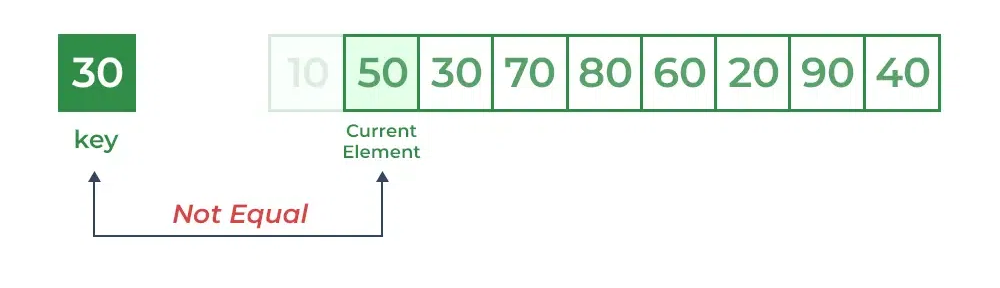
Comparing key with next element arr[1]. Since they are also not equal, the iterator moves to the next element as a potential match.

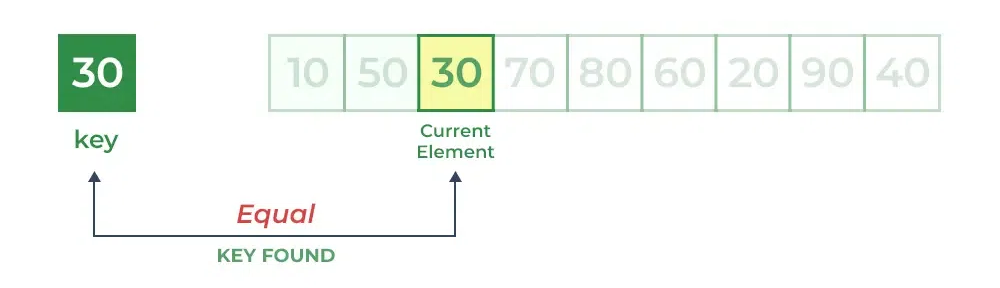
Now when comparing arr[2] with key, the value matches.

So the Linear Search Algorithm will yield a successful message and return the index of the element when key is found (here 2).

If the array elements are not in order, there is no way to search faster than linear/sequential search. We have to look at every element, because otherwise we cannot be certain the element we want is not there. But if the elements are in order, we can use better algorithms!

When we look for a word in a dictionary, we don't just search page by page from front to back.

Since the words are in alphabetical order, you probably want to use a binary search algorithm:

1. Start on a page near the middle of the dictionary.
2. Compare a word on the page to the word you are looking for. If you find it, stop.
3. If the word on the page comes before the word you are looking for, flip to somewhere later in the dictionary and go to step 2.
4. If the word on the page comes after the word you are looking for, flip to somewhere earlier in the dictionary and go to step 2.

If you find two adjacent words on the page and your word comes between them, you can conclude that your word is not in the dictionary.

Binary Search is defined as a searching algorithm used in a sorted array by repeatedly dividing the search interval in half.

Getting back to our previous example of a roster of students, we can write a faster version of search if we know the students are in order (and they usually are!):

public static int binarySearch(String [] roster, String student) {
    int low = 0;
    int high = roster.length - 1;
    while (low <= high) {
        int mid = low + (high - low) / 2; // step 1
        int comp = roster[mid].compareTo(student);
        if (comp == 0) { // step 2
            return mid;
        } else if (comp < 0) { // step 3
            low = mid + 1;
        } else { // step 4
            high = mid - 1;
        }
    }
    return -1;
}

This version is called iterative as the approach iterates through the array.

First, we declare low and high variables to represent the range we are searching. Initially we search the entire array, from 0 to length - 1.

Inside the while loop, we repeat the four steps of binary search:

If low exceeds high, there are no Strings in the range, so we break out of the loop and return -1. Notice that this algorithm depends on the String .compareTo() method.

We can also write this algorithm recursively (the technique of making a method/function call itself):

public static int binarySearch(String [] roster, int low, int high, String student) {
    if (high >= low) {
        int mid = low + (high - low) / 2;
  
        int comp = roster[mid].compareTo(student);
        if (comp == 0)
            return mid;
  
        if (comp < 0)
            return binarySearch(arr, mid + 1, high, x);
        
        return binarySearch(arr, low, mid - 1, x);
      }
  
    return -1;
}

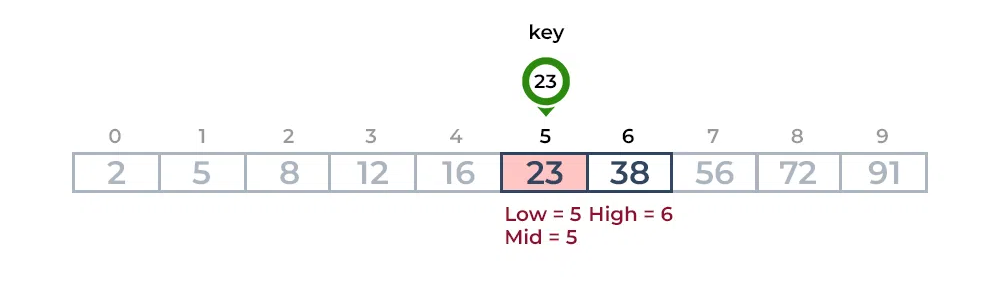
Let's look at another example:

Consider an array int [] arr2 = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}, and the key/target = 23.

The first step: Calculate the mid and compare the mid element with the key. If the key is less than mid element, move to left and if it is greater than the mid then move search space to the right.

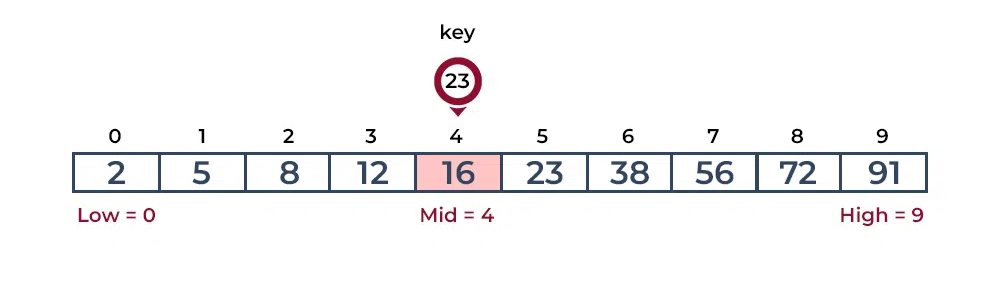
Key (i.e., 23) is greater than current mid element (i.e., 16). The search space moves to the right.

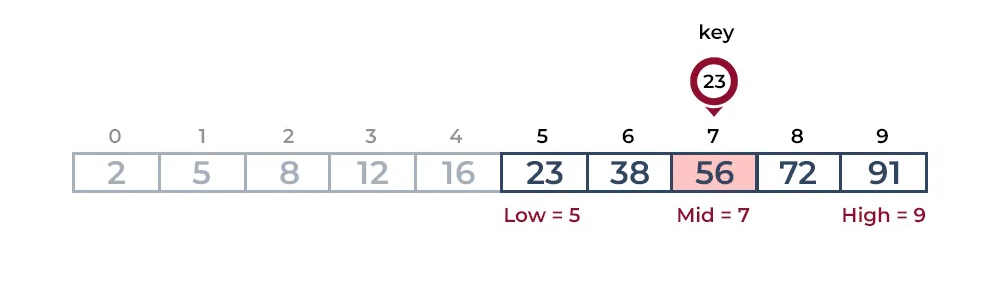
Key is less than the current mid 56. The search space moves to the left.

The second step: If the key matches the value of the mid element, the element is found and stop search.

Documentation on this page is taken from the following:

• Allen Downey and Chris Mayfield, Think Java: How to Think Like a Computer Scientist, 2nd Edition, Version 6.1.3, Green Tea Press, 2016, Creative Commons License.


• GeeksforGeeks


• Programiz


• IOFLOOD